题目内容
16.计算:($\frac{27}{8}$)${\;}^{-\frac{1}{3}}$-cosπ-log2$\root{3}{4}$+${C}_{9}^{7}$=37.分析 化简($\frac{27}{8}$)${\;}^{-\frac{1}{3}}$=$((\frac{3}{2})^{3})^{-\frac{1}{3}}$=$\frac{2}{3}$,cosπ=-1,log2$\root{3}{4}$=$\frac{2}{3}$,${C}_{9}^{7}$=$\frac{9×8}{2×1}$=36,从而求得.
解答 解:∵($\frac{27}{8}$)${\;}^{-\frac{1}{3}}$=$((\frac{3}{2})^{3})^{-\frac{1}{3}}$=$\frac{2}{3}$,cosπ=-1,
log2$\root{3}{4}$=$\frac{2}{3}$,${C}_{9}^{7}$=$\frac{9×8}{2×1}$=36,
∴($\frac{27}{8}$)${\;}^{-\frac{1}{3}}$-cosπ-log2$\root{3}{4}$+${C}_{9}^{7}$=37,
故答案为:37.
点评 本题考查了对数运算与指数运算的应用,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
8.已知函数f(x)=lgx,若f(ab)=10,则f($\frac{1}{a}$)+f($\frac{1}{b}$)=( )
| A. | -10 | B. | $\frac{1}{10}$ | C. | 10 | D. | 20 |
 两点在反比例函数
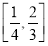
两点在反比例函数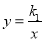 的图象上,
的图象上, 两点在反比例函数
两点在反比例函数 的图象上,
的图象上,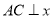 轴于点
轴于点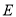 ,
, 轴于点
轴于点 ,
,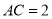 ,
, ,
, ,则
,则 =( )
=( )
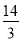 C.
C. D.6[
D.6[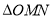 中,
中,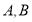 分别是
分别是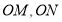 的中点,若
的中点,若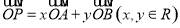 ,且点
,且点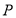 落在四边形
落在四边形 内(含边界),则
内(含边界),则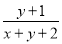 的取值范围是( )
的取值范围是( )
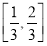 B.
B.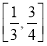 C.
C. D.
D.