题目内容
已知椭圆C: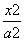 +
+ =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为 时,求k的值.
时,求k的值.
解:(1)由题意得 解得b=
解得b= ,
,
所以椭圆C的方程为 +
+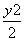 =1.
=1.
(2)由 得(1+2k2)x2-4k2x+2k2-4=0.
得(1+2k2)x2-4k2x+2k2-4=0.
设点M,N的坐标分别为(x1,y1),(x2,y2),则
y1=k(x1-1),y2=k(x2-1),x1+x2= ,
,
 又因为点A(2,0)到直线y=k(x-1)的距离d=
又因为点A(2,0)到直线y=k(x-1)的距离d= ,
,
所以△AMN的面积为S= |MN|·
|MN|· d=
d= .
.
由 =
= ,化简得7k4-2k2-5=0,解得k=±1.
,化简得7k4-2k2-5=0,解得k=±1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
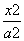 -
-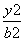 =1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
=1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( ) B.2
B.2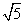
 =1的中心和左焦点,点P为椭圆上的任意一点,则
=1的中心和左焦点,点P为椭圆上的任意一点,则 ·
· 的最大值为( )
的最大值为( ) B.3
B.3 上方,若直线l的倾斜角为60°,则△OAF的面积为________.
上方,若直线l的倾斜角为60°,则△OAF的面积为________. x2+y2-2=0,⊙O′的方程是x2+y2-8x+10=0.由动点P向⊙O和⊙O′所引的切线长相等,则动点P的轨迹方程是________.
x2+y2-2=0,⊙O′的方程是x2+y2-8x+10=0.由动点P向⊙O和⊙O′所引的切线长相等,则动点P的轨迹方程是________. (
( ).
). ;
; 的单调区间.
的单调区间.