题目内容
已知数列{bn}是首项为3,公比为3的等比数列,且bn=
-1(n∈N*).
(1)求数列{an}的通项公式;
(2)若S=an+an+1+…+a2n-1(m∈N*),证明:S<
.
| 1 |
| an |
(1)求数列{an}的通项公式;
(2)若S=an+an+1+…+a2n-1(m∈N*),证明:S<
| 1 |
| 2•3n-1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由数列{bn}是首项为3,公比为3的等比数列,可得bn=3n,利用bn=
-1(n∈N*)即可得出.
(2)S=an+an+1+…+a2n-1=
+
+…+
<
+
+…+
,再利用等比数列的前n项和公式即可得出.
| 1 |
| an |
(2)S=an+an+1+…+a2n-1=
| 1 |
| 3n+1 |
| 1 |
| 3n+1+1 |
| 1 |
| 32n-1+1 |
| 1 |
| 3n |
| 1 |
| 3n+1 |
| 1 |
| 32n-1 |
解答:
解:(1)由数列{bn}是首项为3,公比为3的等比数列,
∴bn=3n,
∵bn=
-1(n∈N*).
∴an=
.
(2)由(1)知:S=an+an+1+…+a2n-1
=
+
+…+
<
+
+…+
=
=
(1-
)<
.
∴bn=3n,
∵bn=
| 1 |
| an |
∴an=
| 1 |
| 3n+1 |
(2)由(1)知:S=an+an+1+…+a2n-1
=
| 1 |
| 3n+1 |
| 1 |
| 3n+1+1 |
| 1 |
| 32n-1+1 |
<
| 1 |
| 3n |
| 1 |
| 3n+1 |
| 1 |
| 32n-1 |
=
| ||||
1-
|
=
| 1 |
| 2×3n-1 |
| 1 |
| 3n |
| 1 |
| 2×3n-1 |
点评:本题考查了等比数列的通项公式及前n项和公式、放缩法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
抛物线y2=4x的焦点坐标为( )
| A、(2,0) |
| B、(1,0) |
| C、(0,-4) |
| D、(-2,0) |
已知函数f(x)=sinx+acosx的图象的一条对称轴是x=
,则函数g(x)=asinx+cosx 的最大值是( )
| 5π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
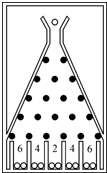 在一块倾斜放置的矩形木块上钉着一个形如“等腰三角形”的五行铁钉,钉子之间留有空隙作为通道,自上而下第1行2个铁钉之间有1个空隙,第2行3个铁钉之间有2个空隙…第5行6个铁钉之间有5个空隙(如图).某人将一个玻璃球从第1行的空隙向下滚动,玻璃球碰到第2行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙,以后玻璃球按类似方式继续往下滚动,落入第5行的某一个空隙后,掉入木板下方相应的球槽.玻璃球落入不同球槽得到的分数ξ如图所示.
在一块倾斜放置的矩形木块上钉着一个形如“等腰三角形”的五行铁钉,钉子之间留有空隙作为通道,自上而下第1行2个铁钉之间有1个空隙,第2行3个铁钉之间有2个空隙…第5行6个铁钉之间有5个空隙(如图).某人将一个玻璃球从第1行的空隙向下滚动,玻璃球碰到第2行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙,以后玻璃球按类似方式继续往下滚动,落入第5行的某一个空隙后,掉入木板下方相应的球槽.玻璃球落入不同球槽得到的分数ξ如图所示.