题目内容
已知椭圆C：
＝1(a>b>0)的两个焦点分别为F1，F2，离心率为
，且过点(2，
)．
(1)求椭圆C的标准方程；
(2)M，N，P，Q是椭圆C上的四个不同的点，两条都不和x轴垂直的直线MN和PQ分别过点F1，F2，且这两条直线互相垂直，求证：
为定值．
（1）
＝1（2）
【解析】(1)由已知，e＝
＝
，所以
＝
＝1－e2＝
，所以a2＝2b2.
所以C：
＝1，即x2＋2y2＝2b2.
因为椭圆C过点(2，
)，代入椭圆方程得b2＝4，所以a2＝8.
所以椭圆C的标准方程为＝1.
(2)证明：由(1)知椭圆的焦点坐标为F1(－2，0)，F2(2，0)．
根据题意，可设直线MN的方程为y＝k(x＋2)，
由于直线MN与直线PQ互相垂直，则直线PQ的方程为y＝－
(x－2)．
设M(x1，y1)，N(x2，y2)．
由方程组
消去y得(2k2＋1)x2＋8k2x＋8k2－8＝0.
则x1＋x2＝
，x1x2＝
.
所以|MN|＝
＝
.同理可得|PQ|＝
.
所以
练习册系列答案
相关题目
某产品的广告费用x与销售额y的统计数据如下表：
广告费用x(万元) | 3 | 4 | 5 | 6 |
销售额y(万元) | 25 | 30 | 40 | 45 |
根据上表可得回归方程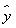
＝
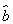x＋
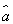中的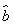
为7.根据此模型，当预报广告费用为10万元时，销售额为________万元．
