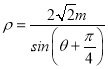Question

【题目】在长方体ABCD﹣A1B1C1D1中，AA1＝2AB＝2AD＝4，过AA1作平面α使BD⊥α，且平面α∩平面A1B1C1D1＝l，M∈l.下面给出了四个命题：这四个命题中，真命题的个数为（ ）

①l∥AC；

②BM⊥AC；

③l和AD1所成的角为60°；

④线段BM长度的最小值为.

A.1B.2C.3D.4

Answer 1

【答案】A

【解析】

①由ABCD﹣A1B1C1D1为长方体，可得BD⊥平面A1ACC1，可得面A1ACC1为平面α，再判断；②结合①根据底面是正方形判断.③利用异面直线所成的角的定义判断.④利用垂线段最短，当M是A1C1的中点时求解判断.

如图所示：

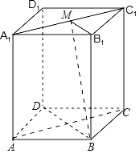
由ABCD﹣A1B1C1D1为长方体，可得BD⊥平面A1ACC1，

即平面A1ACC1为平面α，直线A1C1为l，则l∥AC，故①正确；

由M∈l，即M∈A1C1，只有当M为A1C1的中点时，有BM⊥AC，

当M在l上其它位置时，BM与AC不垂直，故②错误；

由AD1∥BC1，可知∠A1C1B即为l和AD1所成角，

∵A1B＝BC1≠A1C1，∴∠A1C1B≠60°，故③错误；

由A1B＝BC1，可知当M是A1C1的中点时，BM⊥A1C1，

此时线段BM取得最小值，且BM，∴④错误.

故只有①正确.

故选：A.