题目内容
9.在平面直角坐标系xOy中,圆C的参数方程为$\left\{\begin{array}{l}x=cosθ\\ y=-1+sinθ\end{array}\right.(θ$为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的圆心的极坐标为( )| A. | $(1,-\frac{π}{2})$ | B. | (1,π) | C. | (0,-1) | D. | $(1,\frac{π}{2})$ |
分析 圆C的参数方程为$\left\{\begin{array}{l}x=cosθ\\ y=-1+sinθ\end{array}\right.(θ$为参数),化为普通方程:x2+(y+1)2=1,可得圆心C(0,-1),再利用互化公式即可得出.
解答 解:圆C的参数方程为$\left\{\begin{array}{l}x=cosθ\\ y=-1+sinθ\end{array}\right.(θ$为参数),
化为普通方程:x2+(y+1)2=1,可得圆心C(0,-1)
圆C的圆心的极坐标为(1,-$\frac{π}{2}$).
故选:A.
点评 本题考查了圆的参数方程化为普通方程、直角坐标化为极坐标,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
1.如图是某个几何体的三视图,则这个几何体体积是( )
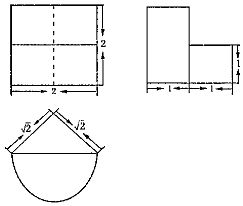

| A. | $2+\frac{π}{2}$ | B. | $2+\frac{π}{3}$ | C. | $4+\frac{π}{3}$ | D. | $4+\frac{π}{2}$ |
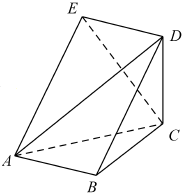 如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.
如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.