题目内容
设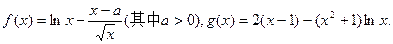
(I)已知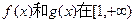 上单调性一致,求a的取值范围;
上单调性一致,求a的取值范围;
(II)设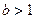 ,证明不等式
,证明不等式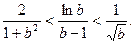
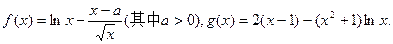
(I)已知
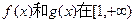 上单调性一致,求a的取值范围;
上单调性一致,求a的取值范围;(II)设
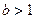 ,证明不等式
,证明不等式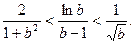
(I)由基本不等式得: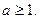
(II)证明见解析。
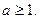
(II)证明见解析。
(I)由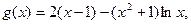
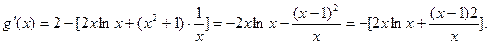 …2分
…2分
当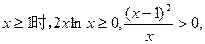
故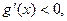
所以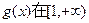 上为减函数。…………4分
上为减函数。…………4分
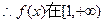 上为减函数,
上为减函数,
由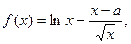 则:
则:
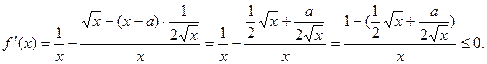 …6分
…6分
在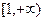 上恒成立,即
上恒成立,即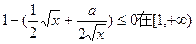 上恒成立;
上恒成立;
即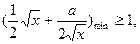
由基本不等式得: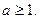 …………8分
…………8分
(II)证明:因为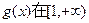 上为减函数,
上为减函数,
又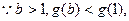
即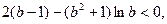 ①…………11分
①…………11分
又当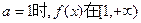 上为减函数。
上为减函数。
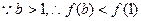
即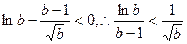 ②
②
由①②可得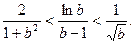 得证。…………15分
得证。…………15分
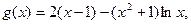
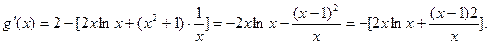 …2分
…2分当
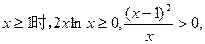
故
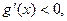
所以
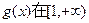 上为减函数。…………4分
上为减函数。…………4分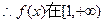 上为减函数,
上为减函数,由
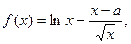 则:
则: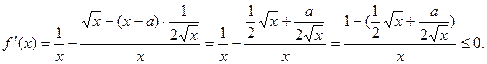 …6分
…6分在
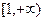 上恒成立,即
上恒成立,即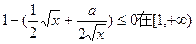 上恒成立;
上恒成立;即
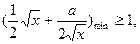
由基本不等式得:
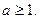 …………8分
…………8分(II)证明:因为
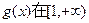 上为减函数,
上为减函数,又
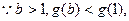
即
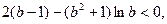 ①…………11分
①…………11分又当
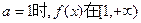 上为减函数。
上为减函数。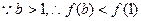
即
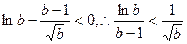 ②
②由①②可得
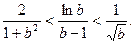 得证。…………15分
得证。…………15分
练习册系列答案
相关题目
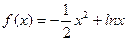 ,
,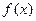 的单调区间;
的单调区间;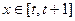
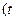 为大于0的常数),求
为大于0的常数),求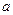 、
、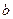 、
、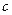 都是实数,函数
都是实数,函数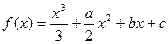 的导函数为
的导函数为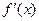
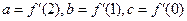 ,求函数
,求函数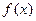 的解析式;
的解析式;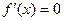 的两个实数根分别为
的两个实数根分别为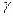 、
、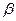 ,并且
,并且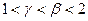
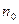 ,使得
,使得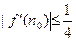 ?请说明理由.
?请说明理由.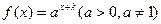 的图象过(-1,1)点,其反函数
的图象过(-1,1)点,其反函数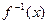 的图象过(8,2)点。
的图象过(8,2)点。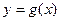 的图象,写出
的图象,写出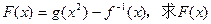 的最小值及取最小值时x的值。
的最小值及取最小值时x的值。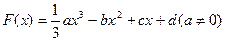 的图象过原点,
的图象过原点,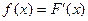 ,
,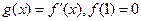 ,函数y=f(x)与y=g(x)的图象交于不同两点A、B。
,函数y=f(x)与y=g(x)的图象交于不同两点A、B。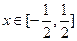 ,求线段AB在x轴上的射影长的取值范围;
,求线段AB在x轴上的射影长的取值范围; 构成的集合:
构成的集合: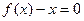 有实根;②函数
有实根;②函数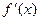 满足0<
满足0<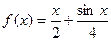 ,判断方程
,判断方程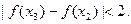
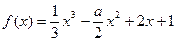 且
且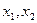 是
是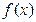 的两个极值点,
的两个极值点,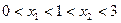 ,
,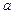 的取值范围;
的取值范围;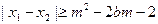 ,对
,对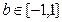 恒成立。求实数
恒成立。求实数 的取值范围;
的取值范围;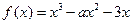 ,
,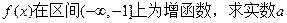 的取值范围;
的取值范围; 的图象与
的图象与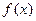 的图象恰有3个交点?若存在求出
的图象恰有3个交点?若存在求出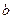 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.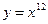 ;(2)
;(2)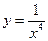 ;(3)
;(3)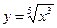 .
.