题目内容
(本小题满分10分)
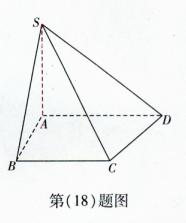
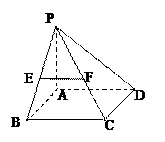
在四棱锥P-ABCD中,底ABCD是矩形, PA⊥面ABCD, AP="AB=2," BC=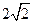 , E、F、G分别为AD、PC、PD的中点.
, E、F、G分别为AD、PC、PD的中点.
(1)求证: FG∥面ABCD
(2)求面BEF与面BAP夹角的大小.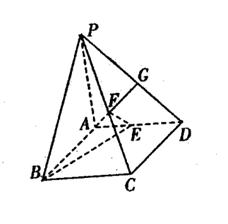
在四棱锥P-ABCD中,底ABCD是矩形, PA⊥面ABCD, AP="AB=2," BC=
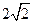 , E、F、G分别为AD、PC、PD的中点.
, E、F、G分别为AD、PC、PD的中点.(1)求证: FG∥面ABCD
(2)求面BEF与面BAP夹角的大小.

(1)略
(2)θ=

解: (1)证明: ∵F、G分别为PC、PD的中点,
∴在△PCD中, FG=∥ CD
CD


(2)分别以AB、AD、AP为空间坐标系的x轴,y轴,z轴,
建立空间坐标系 B(2,0,0), E(0, ,0)F(1,
,0)F(1, ,1), P(0,0,2), D(0,2
,1), P(0,0,2), D(0,2 ,0)
,0)
面BPA的法向量为: , 设面BEF的法向量为m=(x,y,z)
, 设面BEF的法向量为m=(x,y,z)




 ,
,
令 , ∴m="(1,"
, ∴m="(1,"  , -1)
, -1)
∴ 面BAP与面BEF的夹角θ的余 弦为: cosθ=
弦为: cosθ= 
∴ θ=
∴在△PCD中, FG=∥
 CD
CD

(2)分别以AB、AD、AP为空间坐标系的x轴,y轴,z轴,
建立空间坐标系 B(2,0,0), E(0,
 ,0)F(1,
,0)F(1, ,1), P(0,0,2), D(0,2
,1), P(0,0,2), D(0,2 ,0)
,0)面BPA的法向量为:
 , 设面BEF的法向量为m=(x,y,z)
, 设面BEF的法向量为m=(x,y,z)



 ,
, 令
 , ∴m="(1,"
, ∴m="(1,"  , -1)
, -1)∴ 面BAP与面BEF的夹角θ的余
 弦为: cosθ=
弦为: cosθ= 
∴ θ=


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
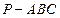 中,
中,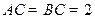 ,
,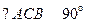 ,侧面
,侧面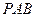 为等边三角形,侧棱
为等边三角形,侧棱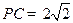 .
.
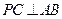 ;
;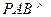 平面
平面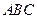 ;
;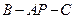 的余弦值
的余弦值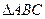 是腰长为2的等腰直角三角形(如图1),
是腰长为2的等腰直角三角形(如图1), ,在边
,在边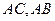 上分别取点
上分别取点 ,使得
,使得 ,把
,把 沿直线
沿直线 折起,使
折起,使 =90°,得四棱锥
=90°,得四棱锥 (如图2).在四棱锥
(如图2).在四棱锥
 (I)求证:CE⊥AF;
(I)求证:CE⊥AF;  时,试在
时,试在 上确定一点G,使得
上确定一点G,使得 ,并证明你的结论.
,并证明你的结论.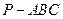 的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥
的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥 中,
中, 平面
平面 ,
,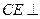 平面
平面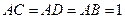 ,
,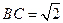 ,
,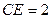 ,
,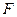 为
为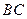 的中点.
的中点.
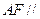 平面
平面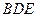 ;
;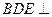 平面
平面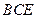 .
.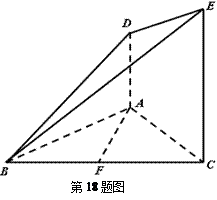
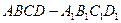 的棱长为
的棱长为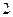 ,
,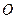 是
是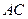 与
与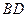 的交点,
的交点,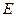 是
是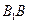 上一点,且
上一点,且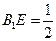 .
.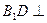 平面
平面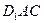 ; (2)求异面直线
; (2)求异面直线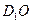 与
与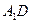 所成角的余弦值;
所成角的余弦值;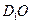 与平面
与平面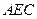 所成角的正弦值.
所成角的正弦值.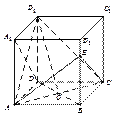
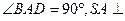 底面ABCD,SA=AB=BC=2,SD与平面ABCD所成角的正切值为
底面ABCD,SA=AB=BC=2,SD与平面ABCD所成角的正切值为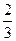 。
。