题目内容
正三棱锥A-BCD内接于球O,且底面边长为
,侧棱长为2,则球O的表面积为
π
π.
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
分析:设三棱锥A-BCD的外接球球心为O,半径为r,由正三棱锥A-BCD内接于球O,且底面边长为
,侧棱长为2,求出球的半径,代入球的表面积公式,可得答案.
| 3 |
解答: 解:如图,设三棱锥A-BCD的外接球球心为O,半径为r,
解:如图,设三棱锥A-BCD的外接球球心为O,半径为r,
BC=CD=BD=
,AB=AC=AD=2,
令AM⊥平面BCD,则M为正△BCD的中心,
则DM=1,AM=
,OA=OD=r,
由图知(
-r)2+1=r2,
解得r=
,
所以S=4πr2=
π.
故答案为:
π
 解:如图,设三棱锥A-BCD的外接球球心为O,半径为r,
解:如图,设三棱锥A-BCD的外接球球心为O,半径为r,BC=CD=BD=
| 3 |
令AM⊥平面BCD,则M为正△BCD的中心,
则DM=1,AM=
| 3 |
由图知(
| 3 |
解得r=
| 2 | ||
|
所以S=4πr2=
| 16 |
| 3 |
故答案为:
| 16 |
| 3 |
点评:本题是基础题,考查空间想象能力,计算能力;求出球的半径是本题解题的关键,仔细观察和分析题意,是解好数学题目的前提.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知正三棱锥A-BCD中,底面边长BC为3,侧棱长AB为
已知正三棱锥A-BCD中,底面边长BC为3,侧棱长AB为 ,求此正三棱锥的体积及内切球的表面积.
,求此正三棱锥的体积及内切球的表面积.
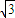 ,侧棱长为2,则球O的表面积为 .
,侧棱长为2,则球O的表面积为 .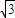 ,侧棱长为2,则球O的表面积为 .
,侧棱长为2,则球O的表面积为 .