题目内容
函数 的最小值是
的最小值是 ,在一个周期内图象最高点与最低点横坐标差是
,在一个周期内图象最高点与最低点横坐标差是 ,又:图象过点
,又:图象过点 ,
,
求(1)函数解析式,
(2)函数的最大值、以及达到最大值时 的集合;
的集合;
(3)该函数图象可由 的图象经过怎样的平移和伸缩得到?
的图象经过怎样的平移和伸缩得到?
(4)当 时,函数的值域.
时,函数的值域.
(1) (2)2 (3)向左平移
(2)2 (3)向左平移 个单位,横坐标伸长到原来的3倍,纵坐标变为原来的2倍 (4)
个单位,横坐标伸长到原来的3倍,纵坐标变为原来的2倍 (4)
解析试题分析:(1)易知:A =" 2" 半周期 ∴T = 6p 即
∴T = 6p 即 (
( ) 从而:
) 从而: 设:
设: 令x = 0 有
令x = 0 有 又:
又: ∴
∴
∴所求函数解析式为 .
.
(2)令 ,即
,即 时,
时, 有最大值2,故当
有最大值2,故当 时,
时, 取最大值2 .
取最大值2 .
(3)因为 ,所以
,所以 向左平移
向左平移 个单位得到
个单位得到 ,横坐标伸长到原来的3倍得到
,横坐标伸长到原来的3倍得到 ,纵坐标伸长到原来的2倍得到
,纵坐标伸长到原来的2倍得到 .
.
(4)因为 ,所以
,所以 ,所以
,所以 ,所以
,所以

 .
.
考点:由 的部分图象确定其解析式.
的部分图象确定其解析式.
点评:本题考查由 的部分图象确定其解析式,确定A,ω,φ的值是关键,φ的确定是难点,属于中档题.
的部分图象确定其解析式,确定A,ω,φ的值是关键,φ的确定是难点,属于中档题.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 为第三象限角,
为第三象限角, .
. ;
;  ,求
,求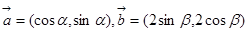 ,且
,且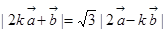 (
(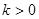 ),设
),设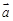 与
与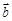 的夹角为
的夹角为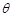
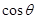 与
与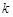 的函数关系式;
的函数关系式;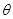 取最大值时,求
取最大值时,求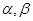 满足的关系式.
满足的关系式. .
. 的最小正周期;
的最小正周期; 中,
中, 分别是
分别是 A、
A、 ,
, ,
, ,求
,求 的值.
的值. ,求
,求 的值;
的值; 为第二象限角,化简
为第二象限角,化简 .
.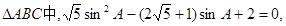 A是锐角,求
A是锐角,求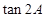 的值;
的值; 的顶点与原点重合,始边与
的顶点与原点重合,始边与 轴非负半轴重合而终边经过点
轴非负半轴重合而终边经过点 .
. 的值;(2)求
的值;(2)求 的值.
的值. 函数
函数

 解析式;
解析式;  的单调递减区间;
的单调递减区间; 上的图像.(要求列表、描点、连线)
上的图像.(要求列表、描点、连线) 上的函数y=f(x)的图象关于直线x=-
上的函数y=f(x)的图象关于直线x=- 对称,当x∈
对称,当x∈ 时,函数f(x)=Asin(ωx+φ)
时,函数f(x)=Asin(ωx+φ)  的图象如图所示.
的图象如图所示.
 的解.
的解.