题目内容
已知定义在区间 上的函数y=f(x)的图象关于直线x=-
上的函数y=f(x)的图象关于直线x=- 对称,当x∈
对称,当x∈ 时,函数f(x)=Asin(ωx+φ)
时,函数f(x)=Asin(ωx+φ)  的图象如图所示.
的图象如图所示.
(1)求函数y=f(x)在 上的表达式;
上的表达式;
(2)求方程f(x)= 的解.
的解.
(1)
(2)x=-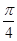 或-
或- 或-
或- 或
或 .
.
解析试题分析:解:(1)当x∈ 时,A=1,
时,A=1, =
= -
- ,T=2π,ω=1.
,T=2π,ω=1.
且f(x)=sin(x+φ)过点 ,
,
则 +φ=π,φ=
+φ=π,φ=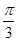 .
.
f(x)=sin .
.
当-π≤x<- 时,-
时,- ≤-x-
≤-x-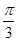 ≤
≤ ,
,
f =sin
=sin ,
,
而函数y=f(x)的图象关于直线x=- 对称,
对称,
则f(x)=f ,
,
即f(x)=sin =-sin x,-π≤x<-
=-sin x,-π≤x<- .
.
∴
(2)当- ≤x≤
≤x≤ 时,
时, ≤x+
≤x+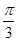 ≤π,
≤π,
由f(x)=sin =
= ,
,
得x+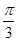 =
=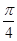 或
或 ,x=-
,x=- 或
或 .
.
当-π≤x<- 时,由f(x)=-sin x=
时,由f(x)=-sin x= ,sin x=-
,sin x=- ,
,
得x=-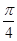 或-
或- .
.
∴x=-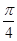 或-
或- 或-
或- 或
或 .
.
考点:三角函数的图像与解析式
点评:解决的关键是根据三角函数的性质来结合图像来得到参数的求解,同事解三角方程,属于基础题。

练习册系列答案
相关题目
 的最小值是
的最小值是 ,在一个周期内图象最高点与最低点横坐标差是
,在一个周期内图象最高点与最低点横坐标差是 ,又:图象过点
,又:图象过点 ,
, 的集合;
的集合; 的图象经过怎样的平移和伸缩得到?
的图象经过怎样的平移和伸缩得到? 时,函数的值域.
时,函数的值域.  ,且
,且 为第三象限角,求
为第三象限角,求 及
及 的值。
的值。 ,计算
,计算 的值
的值
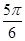 +2α)=
+2α)= ,求f(
,求f( -α)的值.
-α)的值.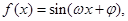 其中
其中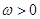 ,
,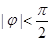
 求
求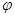 的值;
的值;  的图像的相邻两条对称轴之间的距离等于
的图像的相邻两条对称轴之间的距离等于 ,求函数
,求函数 ,使得函数
,使得函数 中,
中, 、
、 、
、 分别为
分别为 、
、 、
、 所对的角,
所对的角, ,
,  ,
, .
. .
. 中,已知
中,已知 ,
,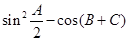 的值;
的值; ,
, ,求
,求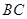 的长。
的长。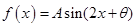 ,其中
,其中 请分别解答以下两小题.
请分别解答以下两小题. ,求函数
,求函数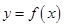 的解析式.
的解析式.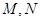 分别是函数
分别是函数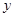 轴两侧与
轴两侧与 轴的两个相邻交点, 函数图像上的一点
轴的两个相邻交点, 函数图像上的一点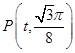 ,若满足
,若满足 ,求函数
,求函数 的最大值.
的最大值.