题目内容

（2008•宁波模拟）已知A（2，1），B（5，5），C（0，4），动点P（x，y）在△ABC内部或边界上，则定点Q（6，3）到点P（x，y）的最小距离为
2
2
．
分析：先根据约束条件画出△ABC内部包括边界，再利用几何意义求最值，只需求出（6，3）到可行域的距离的最小值即可
解答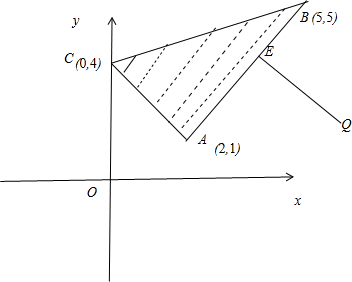：解：根据约束条件画出△ABC内部包括边界，如图所示．
∵A（2，1），B（5，5），
∴AB的方程为：4x-3y-5=0，
从图中可以看出，点到直线AB：4x-3y-5=0的距离即是点Q到点Q到P的距离的最小值
故定点Q（6，3）到点P（x，y）的最小距离：d=
|24-9-5|
5
=2
故答案为：2
点评：本题主要考查了简单的线性规划，点到直线的距离公式的应用以及利用几何意义求最值，属于基础题．
练习册系列答案
相关题目
（2008•宁波模拟）有10件产品，其中3件是次品，从中任取两件，若ξ表示取到次品的个数，则Eξ等于（　　）
（2008•宁波模拟）在等比数列{an}中，a2+a5=18，a3•a4=32，且an+1＜an（n∈N*）
（1）求数列{an}的通项公式；
（2）若Tn=lga1+lga2+…+lgan，求Tn的最大值及此时n的值．
（2008•宁波模拟）已知函数f(x)=Asin(ωx+?)，(A＞0，ω＞0，0＜?＜
π
2
)图象关于点B(-
π
4
，0)对称，点B到函数y=f（x）图象的对称轴的最短距离为
π
2
，且f(
π
2
)=1．
（1）求A，ω，?的值；
（2）若0＜θ＜π，且f(θ)=
1
3
，求cos2θ的值．
（2008•宁波模拟）在等比数列{an}中，若a1+a2+a3=
7
4
，a2=
1
2
，则
1
a1
+
1
a2
+
1
a3
=
13
4
13
4
．
（2008•宁波模拟）在区间（-∞，1）上递增的函数是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网