题目内容
已知α∈R,2sin(π-α)+sin(
+α)=
,则tan2α= .
| π |
| 2 |
| ||
| 2 |
考点:二倍角的正切,运用诱导公式化简求值
专题:三角函数的求值
分析:利用诱导公式化简已知条件,将2sinα+cosα=
两边平方后,利用同角三角函数的基本关系化简得关于tanα的方程,求出tanα的值代入二倍角的正切公式求出tan2α的值.
| ||
| 2 |
解答:
解:α∈R,2sin(π-α)+sin(
+α)=
,
可得2sinα+cosα=
,两边平方得,4sin2α+4sinαcosα+cos2α=
,
即
=
,
则
=
,解得tanα=-3或tanα=
,
所以tan2α=
=
,
故答案为:
.
| π |
| 2 |
| ||
| 2 |
可得2sinα+cosα=
| ||
| 2 |
| 5 |
| 2 |
即
| 4sin2α+4sinαcosα+cos2α |
| sin2α+cos2α |
| 5 |
| 2 |
则
| 4tan2α+4tanα+1 |
| tan2α+1 |
| 5 |
| 2 |
| 1 |
| 3 |
所以tan2α=
| 2tanα |
| 1-tan2α |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查二倍角的正切公式,以及同角三角函数的基本关系的灵活应用,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A、
| ||
B、5
| ||
C、6-2
| ||
D、
|
已知过点A(m,-2)和B(4,m)的直线与直线2x+y-1=0平行,则m的值为( )
| A、-8 | B、0 | C、2 | D、10 |
已知某地区中小学生人数和近视情况分别如图1和图2所示.为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
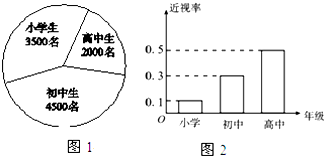

| A、200,20 |
| B、100,20 |
| C、200,10 |
| D、100,10 |
下列函数是偶函数的是( )
| A、y=sinx | ||
| B、y=xsinx | ||
C、y=x
| ||
D、y=2x-
|
已知命题p:?x∈R,x2+x-1<0,则¬p为( )
| A、?x∈R,x2+x-1>0 |
| B、?x∉R,x2+x-1>0 |
| C、?x∉R,x2+x-1≥0 |
| D、?x∈R,x2+x-1≥0 |