题目内容
2.若x,y满足约束条件$\left\{\begin{array}{l}x+2y-2≥0\\ x-y+1≥0\\ 2x+y-4≤0\end{array}\right.$,z=x-2y,则z的取值范围是[-3,2].分析 先作出不等式组表示的平面区域,由z=x-2y可得,y=$\frac{1}{2}$x-$\frac{1}{2}$z,则-$\frac{1}{2}$z表示直线x-2y-z=0在y轴上的截距,截距越大,z越小,结合函数的图形可求z的最大与最小值,从而可求z的范围
解答 解:作出不等式组表示的平面区域:
由z=x-2y可得,y=$\frac{1}{2}$x-$\frac{1}{2}$z,则-$\frac{1}{2}$z表示直线x-2y-z=0在y轴上的截距,截距越大,z越小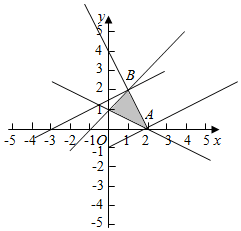
结合函数的图形可知,当直线x-2y-z=0平移到B时,截距最大,z最小;当直线x-2y-z=0平移到A时,截距最小,z最大
由$\left\{\begin{array}{l}{2x+y-4=0}\\{x-y+1=0}\end{array}\right.$可得B(1,2),由$\left\{\begin{array}{l}{x+2y-2=0}\\{2x+y-4=0}\end{array}\right.$,
可得A(2,0)
∴Zmax=2,Zmin=-3
则z=x-2y∈[-3,2]
故答案为:[-3,2].
点评 平面区域的范围问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
17.在随机试验中,在区间[-2,3]内任取一个实数x,则这个数小于1的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
7.已知i为虚数单位,复数z1=1+i,z2=1-i,则$\frac{z_1}{z_2}$=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -i | D. | i |
11.某产品的广告费用x与销售额y的统计数据如表:
根据上表可得回归方程y=bx+a的b为9.2,据此模型预报广告费用为6万元时销售额为( )
| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | 54 |
| A. | 63.6万 | B. | 65万 | C. | 66.1万 | D. | 67.7万 |