题目内容
12．已知a1=1，a2=3，an=an-1-an-2（n≥3），则a2016=-2．分析 由已知数列递推式求得数列前几项，可得数列{an}是以6为周期的周期数列，由此求得答案．
解答 解：由a1=1，a2=3，an=an-1-an-2，得
a3=a2-a1=3-1=2，a4=a3-a2=2-3=-1，
a5=a4-a3=-1-2=-3，a6=a5-a4=-3-（-1）=-2，
a7=a6-a5=-2-（-3）=1，…
由上可知，数列{an}是以6为周期的周期数列，
则a2016=a336×6=a6=-2．
故答案为：-2．
点评 本题考查数列递推式，考查了数列的函数特性，关键是对数列周期的发现，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图，在圆x2+y2=1上任取一点P，过点P作x轴的垂线段DM，D为垂足，点P为线段DM的中点．
1．已知函数f（x）=sinx（-$\frac{π}{2}$$＜x＜\frac{π}{2}$），满足f（x）＜$\frac{\sqrt{3}}{2}$的x的取值范围是（ ）
| A． | （-$\frac{π}{6}$，$\frac{π}{6}$） | B． | （-$\frac{π}{2}$，$\frac{π}{6}$） | C． | （-$\frac{π}{2}$，$\frac{π}{3}$） | D． | （-$\frac{π}{3}$，$\frac{π}{3}$） |
16．
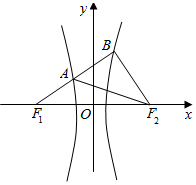已知F1，F2分别为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点，若存在过F1的直线分别交双曲线C的左、右支于A，B两点，使得∠BAF2=∠BF2F1，则双曲线C的离心率e的取值范围是（ ）
已知F1，F2分别为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点，若存在过F1的直线分别交双曲线C的左、右支于A，B两点，使得∠BAF2=∠BF2F1，则双曲线C的离心率e的取值范围是（ ）| A． | （3，+∞） | B． | （1，2+$\sqrt{5}$） | C． | （3，2+$\sqrt{5}$） | D． | （1，3） |