题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为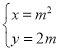 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(Ⅱ)已知点![]() 设直线
设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(Ⅰ)直线![]() 的直角坐标方程为
的直角坐标方程为![]() ;曲线
;曲线![]() 的普通方程为
的普通方程为![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(I)利用参数方程、普通方程、极坐标方程间的互化公式即可;
(II)将直线参数方程代入抛物线的普通方程,可得![]() ,而根据直线参数方程的几何意义,知
,而根据直线参数方程的几何意义,知 ,代入即可解决.
,代入即可解决.
![]() 由
由![]()
可得直线![]() 的直角坐标方程为
的直角坐标方程为![]()
由曲线![]() 的参数方程,消去参数
的参数方程,消去参数![]()
可得曲线![]() 的普通方程为
的普通方程为![]() .
.
![]() 易知点
易知点![]() 在直线
在直线![]() 上,直线
上,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的普通方程,并整理得
的普通方程,并整理得![]() .
.
设![]() 是方程
是方程![]() 的两根,则有
的两根,则有![]() .
.



 口算题天天练系列答案
口算题天天练系列答案【题目】某地区高考实行新方案,规定:语文、数学和英语是学生的必考科目,学生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生确定选考方案,否则称该学生待确定选考方案.例如学生甲选择“物理、化学和生物”三个选考科目,则称学生甲确定选考方案.某校为了解高一年级![]() 名学生选考科目的意向,随机选取
名学生选考科目的意向,随机选取![]() 名学生进行了一次调查,统计情况如下表:
名学生进行了一次调查,统计情况如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男 生 | 选考方案确定的有 |
|
|
|
|
|
|
选考方案待确定的有 |
|
|
|
|
|
| |
女 生 | 选考方案确定的有 |
|
|
|
|
|
|
选考方案待确定的有 |
|
|
|
|
|
|
(1)估计该校高一年级已确定选考方案的学生有多少人?
(2)假设男生、女生选择选考科目是相互独立的.从确定选考方案的![]() 名男生中随机选出
名男生中随机选出![]() 名,从确定选考方案的
名,从确定选考方案的![]() 名女生中随机选出
名女生中随机选出![]() 名,试求该男生和该女生的选考方案中都含有历史科目的概率;
名,试求该男生和该女生的选考方案中都含有历史科目的概率;
(3)从确定选考方案的8名男生中随机选出2名,设随机变量![]() 表示
表示![]() 名男生选考方案相同,
名男生选考方案相同,![]() 表示
表示![]() 名男生选考方案不同,求
名男生选考方案不同,求![]() 的分布列及数学期望.
的分布列及数学期望.
