题目内容
已知α,β∈(0,π),且tan(α-β)=
,tanβ=-
(1)计算tanα、tan2α的值
(2)求2α-β的值.
| 1 |
| 2 |
| 1 |
| 7 |
(1)计算tanα、tan2α的值
(2)求2α-β的值.
(1)∵tan(α-β)=
,∴
=
…(2分)
而:tanβ=-
,∴
=
,解得tanα=
…(5分)
∴tan2α=
=
=
…(7分)
(2)tan(2α-β)=
=
=1.…(9分)
∵tanα=
>0,α∈(0,π),∴0<α<
,0<2α<π
∵tan2α=
>0∴0<2α<
,…(11分)
∵tanβ=-
<0,β∈(0,π),∴
<β<π,…(12分)
∴-π<2α-β<0,…(13分)
∴2α-β=-
.…(15分)
| 1 |
| 2 |
| tanα-tanβ |
| 1+tanαtanβ |
| 1 |
| 2 |
而:tanβ=-
| 1 |
| 7 |
tanα+
| ||
1-
|
| 1 |
| 2 |
| 1 |
| 3 |
∴tan2α=
| 2tanα |
| 1-tan2α |
2×
| ||
1-(
|
| 3 |
| 4 |
(2)tan(2α-β)=
| tan2α-tanβ |
| 1+tan2αtanβ |
| ||||
1-
|
∵tanα=
| 1 |
| 3 |
| π |
| 2 |
∵tan2α=
| 3 |
| 4 |
| π |
| 2 |
∵tanβ=-
| 1 |
| 7 |
| π |
| 2 |
∴-π<2α-β<0,…(13分)
∴2α-β=-
| 3π |
| 4 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
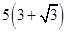 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距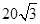 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?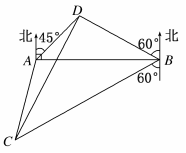
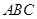 中,已知
中,已知 ,向量
,向量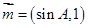 ,
,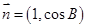 ,且
,且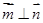 .
.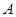 的值;
的值;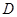 在边
在边 上,且
上,且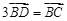 ,
,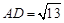 ,求△
,求△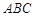 的面积.
的面积.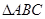 中,若
中,若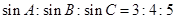 ,则
,则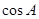 的值为
的值为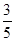
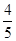

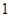
 =" " .
=" " .