题目内容
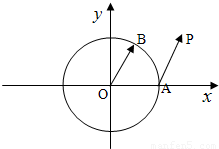
 已知单位圆⊙O:x2+y2=1,A(1,0),B是圆上的动点,
已知单位圆⊙O:x2+y2=1,A(1,0),B是圆上的动点, ∥
∥ ,
, .
.
(1)求点P的轨迹E的方程;
(2)求过A作直线l被E截得的弦长的最小值.
解:(1)设P(x,y),B(m,n),则
∵ ∥
∥ ,
, .
.
∴my=n(x-1),(m-1)(x-1)+ny=1
∴
∵m2+n2=1
∴y2=2x-1
(2)设直线方程为x=my+1,代入抛物线方程可得y2-2my-1=0,则△=4m2+4>0
设过A作直线l被E截得的弦的端点A(x1,y1),B(x2,y2),
∴y1+y2=2m,y1y2=-1
∴|AB|=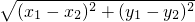 =2(1+m2)≥2(当且仅当m=0时取等号)
=2(1+m2)≥2(当且仅当m=0时取等号)
∴过A作直线l被E截得的弦长的最小值为2.
分析:(1)设P(x,y),B(m,n),用坐标表示向量,根据 ∥
∥ ,
, ,可得
,可得 ,利用点B在单位圆上,即可点P的轨迹E的方程;
,利用点B在单位圆上,即可点P的轨迹E的方程;
(2)设直线方程为x=my+1,代入抛物线方程可得y2-2my-1=0,利用韦达定理及弦长公式,即可求得过A作直线l被E截得的弦长的最小值.
点评:本题考查向量知识的运用,考查轨迹方程的求解,考查弦长公式,考查直线与抛物线的位置关系,属于中档题.

∵
 ∥
∥ ,
, .
.∴my=n(x-1),(m-1)(x-1)+ny=1
∴

∵m2+n2=1
∴y2=2x-1
(2)设直线方程为x=my+1,代入抛物线方程可得y2-2my-1=0,则△=4m2+4>0
设过A作直线l被E截得的弦的端点A(x1,y1),B(x2,y2),
∴y1+y2=2m,y1y2=-1
∴|AB|=
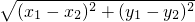 =2(1+m2)≥2(当且仅当m=0时取等号)
=2(1+m2)≥2(当且仅当m=0时取等号)∴过A作直线l被E截得的弦长的最小值为2.
分析:(1)设P(x,y),B(m,n),用坐标表示向量,根据
 ∥
∥ ,
, ,可得
,可得 ,利用点B在单位圆上,即可点P的轨迹E的方程;
,利用点B在单位圆上,即可点P的轨迹E的方程;(2)设直线方程为x=my+1,代入抛物线方程可得y2-2my-1=0,利用韦达定理及弦长公式,即可求得过A作直线l被E截得的弦长的最小值.
点评:本题考查向量知识的运用,考查轨迹方程的求解,考查弦长公式,考查直线与抛物线的位置关系,属于中档题.

练习册系列答案
相关题目
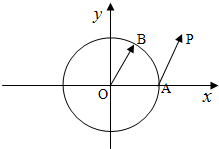 已知单位圆⊙O:x2+y2=1,A(1,0),B是圆上的动点,
已知单位圆⊙O:x2+y2=1,A(1,0),B是圆上的动点,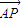 ∥
∥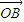 ,
,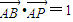 .
.