题目内容
18.已知A(-1,2),B(-2,4),则直线AB的斜率为( )| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
分析 根据题意,将点A、B的坐标代入直线的斜率公式计算即可得答案.
解答 解:根据题意,已知A(-1,2),B(-2,4),
则直线AB的斜率k=$\frac{4-2}{(-2)-(-1)}$=-2;
故选:A.
点评 本题考查直线的斜率计算,关键是掌握直线的斜率计算公式.

练习册系列答案
相关题目
8.曲线f(x)=x2+lnx上任意一点的切线为l1,曲线g(x)=ex-ax上总有一条切线l2与l1平行,则a的取值范围是( )
| A. | $(-2\sqrt{2},2\sqrt{2})$ | B. | $(-∞,-2\sqrt{2})$ | C. | $(-2\sqrt{2},+∞)$ | D. | $[-2\sqrt{2},2\sqrt{2}]$ |
9.函数$f(x)=\frac{x^3}{3}+\frac{1}{x}$的导数f'(x)=( )
| A. | $\frac{x^2}{3}+\frac{1}{x}$ | B. | ${x^2}-\frac{1}{x^2}$ | C. | $-{x^2}-\frac{1}{x^2}$ | D. | x2+lnx |
3.已知函数f(x)=Asin(ωx+φ)( A>0,ω>0,$|φ|<\frac{π}{2}$)在一个周期内的图象如图所示,则$f({\frac{π}{6}})$=( )
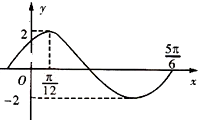

| A. | 1 | B. | $\sqrt{3}$ | C. | -1 | D. | $-\sqrt{3}$ |
10.从1,2,3,4中任取两个数,记作a,b,则两数之和a+b小于5的概率为( )
| A. | $\frac{5}{6}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |