题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,则方程$f(x)=\frac{1}{2}$的解集为( )| A. | $\{\sqrt{2},-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}\}$ | B. | $\{\sqrt{2},\frac{{\sqrt{2}}}{2}\}$ | C. | $\{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}\}$ | D. | $\{\sqrt{2},-\frac{{\sqrt{2}}}{2}\}$ |
分析 利用分段函数,分段代入求解,即可得出结论.
解答 解:x≤0,${x}^{2}=\frac{1}{2}$,∴x=-$\frac{\sqrt{2}}{2}$,
x>0,$lo{g}_{2}x=\frac{1}{2}$,∴x=$\sqrt{2}$,
∴方程$f(x)=\frac{1}{2}$的解集为{$\sqrt{2}$,-$\frac{\sqrt{2}}{2}$}.
故选D
点评 本题考查分段函数,考查方程的解,正确理解分段函数是关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
19.已知点A(-2,3)在抛物线C:y2=2px的准线上,记C的焦点为F,则直线AF的斜率为( )
| A. | -2 | B. | -$\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{1}{2}$ |
8.曲线f(x)=x2+lnx上任意一点的切线为l1,曲线g(x)=ex-ax上总有一条切线l2与l1平行,则a的取值范围是( )
| A. | $(-2\sqrt{2},2\sqrt{2})$ | B. | $(-∞,-2\sqrt{2})$ | C. | $(-2\sqrt{2},+∞)$ | D. | $[-2\sqrt{2},2\sqrt{2}]$ |
18.将函数$y=sin(\frac{1}{2}x-\frac{π}{6})$的图象上的所有的点横坐标缩短为原来的$\frac{1}{2}$(纵坐标不变),再将所得的图象向右平移$\frac{π}{3}$个单位,则所得的函数图象对应的解析式为( )
| A. | $y=cos(\frac{1}{4}x-\frac{π}{4})$ | B. | y=-sinx | C. | y=-cosx | D. | $y=sin(x+\frac{π}{6})$ |
3.已知函数f(x)=Asin(ωx+φ)( A>0,ω>0,$|φ|<\frac{π}{2}$)在一个周期内的图象如图所示,则$f({\frac{π}{6}})$=( )
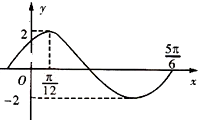

| A. | 1 | B. | $\sqrt{3}$ | C. | -1 | D. | $-\sqrt{3}$ |