题目内容
若f(a+b)=f(a)•f(b)且f(1)=2.则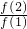 +
+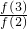 +…+
+…+ =________.
=________.
4022
分析:由已知f(a+b)=f(a)•f(b)可得f(n+1)=f(n)f(1),即可得 =f(1)=2,把n=1,2,3,4,5…2011分别代入可求.
=f(1)=2,把n=1,2,3,4,5…2011分别代入可求.
解答:令b=1.∴f(a+1)=f(a)f(1)
∴ =f(1)=2
=f(1)=2
∴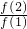 =2.
=2.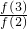 =2.…
=2.… =2
=2
∴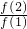 +
+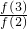 +…+
+…+ =2011×2=4022.答案:4022.
=2011×2=4022.答案:4022.
点评:本题主要考查了利用抽象函数满足的性质求解函数的函数值,解题的 关键是由已知利用赋值得到 =f(1)=2.
=f(1)=2.
分析:由已知f(a+b)=f(a)•f(b)可得f(n+1)=f(n)f(1),即可得
 =f(1)=2,把n=1,2,3,4,5…2011分别代入可求.
=f(1)=2,把n=1,2,3,4,5…2011分别代入可求.解答:令b=1.∴f(a+1)=f(a)f(1)
∴
 =f(1)=2
=f(1)=2∴
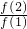 =2.
=2.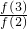 =2.…
=2.… =2
=2∴
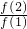 +
+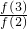 +…+
+…+ =2011×2=4022.答案:4022.
=2011×2=4022.答案:4022.点评:本题主要考查了利用抽象函数满足的性质求解函数的函数值,解题的 关键是由已知利用赋值得到
 =f(1)=2.
=f(1)=2. 
练习册系列答案
相关题目
函数f(x)=-x2+ax+b,若f(1)=f(3),则下面正确的说法是( )
| A、f(0)<f(5)<f(2) | B、f(5)<f(0)<f(2) | C、f(2)<f(0)<f(5) | D、f(0)<f(2)<f(5) |