已知在等比数列{an}中.a2.a10是方程x2-8x+9=0的两根.则a6为( )A．-3B．±3C．3D．2 题目和参考答案——青夏教育精英家教网—

题目内容

14．已知在等比数列{a_n}中，a₂，a₁₀是方程x²-8x+9=0的两根，则a₆为（　　）

A．

-3

B．

±3

C．

D．

分析利用一元二次方程根与系数的关系可得a₂+a₁₀=8，a₂a₁₀=9，进一步得到a₂＞0，a₁₀＞0，再由等比数列的性质得答案．

解答解：由题意可得，a₂+a₁₀=8，a₂a₁₀=9，
∴a₂＞0，a₁₀＞0，
由等比数列的性质可得：${{a}_{6}}^{2}={a}_{2}{a}_{10}=9$．
则a₆=-3（舍）或a₆=3．
故选：C．

点评本题考查等比数列的性质，训练了根与系数的关系的应用，是基础题．

练习册系列答案

相关题目

4．

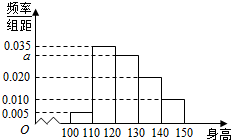从某小学随机抽取200名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）．若要从身高在[120，130），[130，140），[140，150]三组内的学生中，用分层抽样的方法选取36人参加一项活动，则从身高在[140，150]内的学生中选取的人数应为（　　）

5．已知α是第一象限角，且$f（α）=\frac{{sin（{\frac{π}{2}-α}）cos（{\frac{3π}{2}+α}）tan（{π+α}）}}{{tan（{-π-α}）sin（{π-α}）}}$
（1）化简f（α）；
（2）若$sinα=\frac{1}{5}$，求f（α）的值．

2．已知圆C：（x-1）²+（y-2）²=25，直线l：（2m+1）x+（m+1）y-7m-4=0．
（1）求证：直线l恒过定点；
（2）求直线l被圆C截得的弦长最长与最短的方程．

9．建造一个容积为240m³，深为5m的长方体无盖蓄水池，池壁的造价为180元/m²，池底的造价为350元/m²，如何设计水池的长与宽，才能使水池的总造价为42000元？

19．设f₀（x）=sinx，f₁（x）=f₀′（x），f₂（x）=f₁′（x），…，f_n+1（x）=f_n′（x），n∈N，则f₂₀₁₆（x）=（　　）

6．在（1+x）³+（1+x）⁴+…+（1+x）²⁰⁰⁷的展开式中，x³的系数等于（　　）

3．数列{a_n}是公差d不为0的等差数列，a₁=2，S_n为其前n项和．
（1）当a₃=6时，若a₁，a₃，a${\;}_{{n}_{1}}$，a${\;}_{{n}_{2}}$…，a${\;}_{{n}_{k}}$成等比数列（其中3＜n₁＜n₂＜…＜n_k），求n_k的表达式；
（2）是否存在合适的公差d，使得{a_n}的任意前3n项中，前n项的和与后n项的和的比值等于定常数？求出d，若不存在，说明理由．

4．（1）设a，b，c均为正数，求证：$a+\frac{1}{b}，b+\frac{1}{c}，c+\frac{1}{a}$中至少有一个不小于2；
（2）设函数f（x）=ln（1+x），g（x）=xf′（x），x≥0（其中f′（x）是f（x）导函数）．已知g₁（x）=g（x），g_n+1（x）=g（g_n（x）n∈N^*．
（1）求g₁（x），g₂（x）；
（2）猜想g_n（x）表达式，并用数学归纳法证明．

试题分类