题目内容
2.已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.(1)求证:直线l恒过定点;
(2)求直线l被圆C截得的弦长最长与最短的方程.
分析 (1)通过直线l转化为直线系,求出直线恒过的定点;
(2)说明直线l被圆C截得的弦长最小时,圆心与定点连线与直线l垂直,求出斜率即可求出m的值,再由勾股定理即可得到最短弦长.
解答 (1)证明:将直线化为直线束方程:x+y-4+(2x+y-7)=0.联立方程x+y-4=0与2x+y-7=0,得点(3,1);
将点(3,1)代入直线方程,不论m为何值时都满足方程,所以直线l恒过定点(3,1);
(2)解:当直线l过圆心与定点(3,1)时,弦长最大,代入圆心坐标得m=$\frac{1}{3}$.
当直线l垂直于圆心与定点(3,1)所在直线时弦长最短,斜率为2,代入方程得m=$-\frac{3}{4}$
此时直线l方程为2x-y-5=0,圆心到直线的距离为$\sqrt{5}$,所以最短弦长为$4\sqrt{5}$.
点评 本题考查直线系方程的应用,考查直线与圆的位置关系,考查平面几何知识的运用,考查计算能力,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
10.若$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(-6,3),则2$\overrightarrow{a}$+$\overrightarrow{b}$=( )
| A. | (-2,1) | B. | (-4,6) | C. | (-4,-2) | D. | (10,-5) |
17.某班主任对全班50名学生的积极性和对待班级工作的态度进行了调查,统计数据如表所示:
试运用独立性检验的思想方法分析:能否有99.5%的把握认为学生的学习积极性与对待班级工作的态度有关系?说明理由.
| 积极参加班级工作 | 不太积极参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
14.已知在等比数列{an}中,a2,a10是方程x2-8x+9=0的两根,则a6为( )
| A. | -3 | B. | ±3 | C. | 3 | D. | 2 |
11.在△ABC中,b=5,c=5$\sqrt{3}$,A=30°,则a等于( )
| A. | 5 | B. | 4 | C. | 3 | D. | 10 |
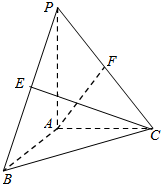 (理科做)如图,在三棱锥P-ABC中,已知PA⊥平面ABC,∠BAC=$\frac{π}{2}$,PA=AB=AC,E,F分别为棱PB,PC的中点,则异面直线AF与CE所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
(理科做)如图,在三棱锥P-ABC中,已知PA⊥平面ABC,∠BAC=$\frac{π}{2}$,PA=AB=AC,E,F分别为棱PB,PC的中点,则异面直线AF与CE所成的角的余弦值为$\frac{\sqrt{3}}{6}$.