题目内容
【题目】设椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为
,上顶点为![]() ,过
,过![]() 与
与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于
轴负半轴于![]() 点,且
点,且![]() 恰好是线段
恰好是线段![]() 的中点.
的中点.
(1)若过![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() 相切,求椭圆
相切,求椭圆![]() 的方程;
的方程;
(2)在(1)的条件下, ![]() 是椭圆
是椭圆![]() 的左顶点,过点
的左顶点,过点![]() 作与
作与![]() 轴不重合的直线
轴不重合的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 分别交直线
分别交直线![]() 于
于![]() 两点,若直线
两点,若直线![]() 的斜率分别为
的斜率分别为![]() ,试问:
,试问: ![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 为定值,且定值为
为定值,且定值为![]() .
.
【解析】【试题分析】(1)依据题设条件建立方程求解;(2)运用直线与椭圆的位置关系进行分析推证:
解析:(1)由题意知: ![]() ,
, ![]() 是线段
是线段![]() 的中点,设
的中点,设![]() ,
, ![]() ,则
,则![]() ,因为
,因为![]() ,
,
所以![]() .
.
由题意知: ![]() 外接圆的圆心为斜边
外接圆的圆心为斜边![]() 的中点
的中点![]() ,半径等于
,半径等于![]() .
.
因为过![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() 相切,所以
相切,所以![]() 到直线的距离等于半径
到直线的距离等于半径![]() ,即
,即![]() ,解得
,解得![]() ,
, ![]() ,
, ![]() ,
,
所以,椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,直线
,直线![]() 的方程为
的方程为![]() ,由
,由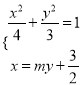 消去
消去![]() 得:
得:
![]() ,
,
所以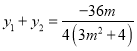 ,
, 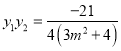 ,
,
由![]() 三点共线可知:
三点共线可知: 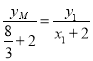 ,即
,即![]() ,
,
同理可得: ![]() ,所以
,所以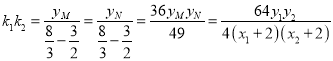 ,
,
因为![]() ,
,
所以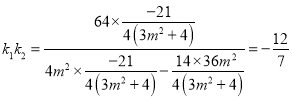 ,故
,故![]() 为定值,且定值为
为定值,且定值为![]()

 阅读快车系列答案
阅读快车系列答案【题目】某种多面体玩具共有12个面,在其十二个面上分别标有数字1,2,3,…,12.若该玩具质地均匀,则抛掷该玩具后,任何一个数字所在的面朝上的概率均相等.
为检验某批玩具是否合格,制定检验标准为:多次抛掷该玩具,并记录朝上的面上标记的数字,若各数字出现的频率的极差不超过0.05.则认为该玩具合格.

(1)对某批玩具中随机抽取20件进行检验,将每个玩具各面数字出现频率的极差绘制成茎叶图(如图所示),试估计这批玩具的合格率;
(2)现有该种类玩具一个,将其抛掷100次,并记录朝上的一面标记的数字,得到如下数据:
朝上面的数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
次数 | 9 | 7 | 8 | 6 | 10 | 9 | 9 | 8 | 10 | 9 | 7 | 8 |
1)试判定该玩具是否合格;
2)将该玩具抛掷一次,记事件![]() :向上的面标记数字是完全平方数(能写成整数的平方形式的数,如
:向上的面标记数字是完全平方数(能写成整数的平方形式的数,如![]() ,9为完全平方数);事件
,9为完全平方数);事件![]() :向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中
:向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中![]() 表示
表示![]() 的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件
的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件![]() 与事件
与事件![]() 有关.
有关.
|
| 合计 | |
| |||
| |||
合计 | 100 |
(参考公式及数据:![]() ,
,![]() )
)