题目内容
(本小题12分) 已知 为实数,
为实数, ,
,
(1)若 ,求
,求 的单调区间;
的单调区间;
(2)若 ,求
,求 在[-2,2] 上的最大值和最小值。
在[-2,2] 上的最大值和最小值。
(1) 的递增区间为
的递增区间为 ,
, 递减区间为
递减区间为
(2) f(x)在[-2,2]上的最大值为 最小值为
最小值为
解析试题分析:(1)当 时,
时,

由 ,得
,得 或
或
由 ,得
,得
所以 的递增区间为
的递增区间为 ,
, 递减区间为
递减区间为 (6分)
(6分)
(2) ∴
∴
由 得
得 ,所以
,所以
 ,令
,令 得
得 或x="-1"
或x="-1"
列表格,或者讨论单调性,求出极值。再比较端点值。
又
所以f(x)在[-2,2]上的最大值为 最小值为
最小值为 (12分)
(12分)
考点:函数的单调性,以及函数的最值
点评:考查了导数在解决函数单调性和极值的运用,同时能结合函数的极值得到最值,属于基础题。

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
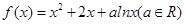 .
.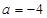 时,求
时,求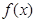 的最小值;
的最小值;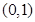 上为单调函数,求实数
上为单调函数,求实数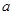 的取值范围;
的取值范围;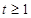 时,不等式
时,不等式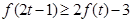 恒成立,求实数
恒成立,求实数 .
. 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值; 在区间
在区间 上是单调递减函数,求实数
上是单调递减函数,求实数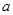 的取值范围.
的取值范围. 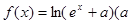 为常数,
为常数,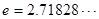 )是
)是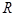 上的奇函数.
上的奇函数.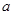 的值;(Ⅱ)讨论关于
的值;(Ⅱ)讨论关于 的方程
的方程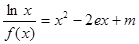 的根的个.
的根的个.
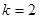 时,求曲线
时,求曲线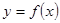 在点
在点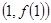 处的切线方程。
处的切线方程。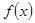 的单调区间
的单调区间 是
是 的一个极值点
的一个极值点 的值;
的值; 的单调增区间;
的单调增区间; ,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?
,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么? ,求
,求 。
。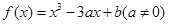 .
.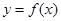 在点
在点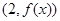 处与直线
处与直线 相切,求
相切,求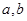 的值;
的值;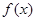 的单调区间与极值点.
的单调区间与极值点.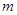 是实数,
是实数,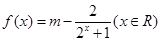 ,
, 为奇函数,求
为奇函数,求 上为单调递增函数;
上为单调递增函数;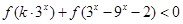 对任意
对任意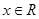 恒成立,求实数
恒成立,求实数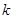 的取值范围。
的取值范围。