题目内容
已知函数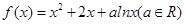 .
.
(1)当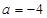 时,求
时,求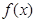 的最小值;
的最小值;
(2)若函数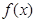 在区间
在区间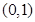 上为单调函数,求实数
上为单调函数,求实数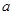 的取值范围;
的取值范围;
(3)当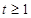 时,不等式
时,不等式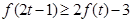 恒成立,求实数
恒成立,求实数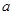 的取值范围.
的取值范围.
(1) 3.(2) 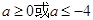 .(3)
.(3) 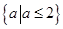 .
.
解析试题分析:(1) 当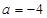 时,
时, 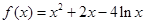
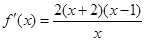
当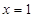 时 函数
时 函数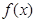 取最小值3.
取最小值3.
(2) 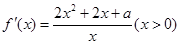 设
设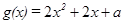
依题意 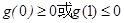 得
得 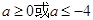 .
.
(3) 当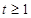 时
时 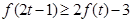 恒成立
恒成立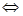 当
当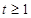 时
时 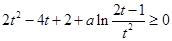 恒成立
恒成立
设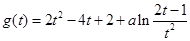 则
则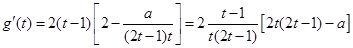

(1)当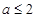 时,
时,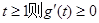
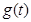 在
在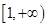 单调递增,
单调递增,
(2)当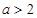 时,设
时,设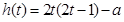

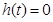 有两个根,一个根大于1,一个根小于1.
有两个根,一个根大于1,一个根小于1.
不妨设 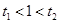
当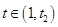 时
时 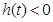 即
即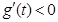
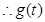 在
在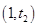 单调递减
单调递减 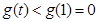
不满足已知条件.
综上: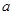 的取值范围为
的取值范围为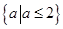 .
.
考点:本题考查了导数的运用
点评:此类问题是在知识的交汇点处命题,将函数、导数、不等式、方程的知识融合在一起进行考查,重点考查了利用导数研究函数的极值与最值等知识

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
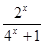 .
. 的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
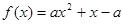
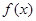 有最 大值
有最 大值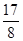 ,求实数
,求实数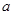 的值
的值
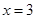 是函数
是函数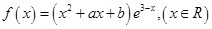 的一个极值点。
的一个极值点。 与
与 的关系式(用
的关系式(用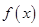 的单调区间;
的单调区间;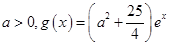 ,若存在
,若存在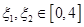 ,使得
,使得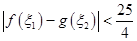 成立,求实数
成立,求实数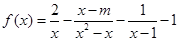
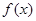 无零点,求实数
无零点,求实数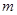 的取值范围;
的取值范围;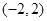 有且仅有一个零点,求实数
有且仅有一个零点,求实数
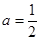 时,求函数
时,求函数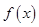 的值域;
的值域;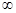 ,+
,+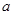 的高考资源网取值范围.
的高考资源网取值范围.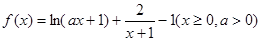 。
。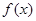 在
在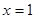 处取得极值,求
处取得极值,求 的值;
的值;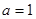 且
且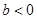 ,函数
,函数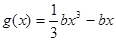 ,若对于
,若对于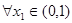 ,总存在
,总存在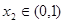 使得
使得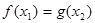 ,求实数
,求实数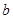 的取值范围。
的取值范围。 为实数,
为实数, ,
, ,求
,求 的单调区间;
的单调区间; ,求
,求