题目内容

（1）化简：
1-2sin100°cos280°
1-cos2170°
-cos370°
．
（2）已知：sinαcosα=
1
4
，且
π
4
＜α＜
π
2
，求cosα-sinα的值．
（1）原式=
1-2cos10°sin10°
sin210°
-cos10°
=
(cos10°-sin10)2
sin10°-cos10°
=
cos10°-sin10°
sin10°-cos10°
=1
（2）∵（sinα-cosα）2=sin2α-2sinαcosα+cos2α
=（sin2α+cos2α）-2sinαcosα；
又∵sin2α+cos2α=1，sinαcosα=
1
4

∴（sinα-cosα）2=1-2×
1
4
=
1
2

∵
π
4
＜α＜
π
2

∴cosα-sinα=-
2
2
练习册系列答案
相关题目
求所给函数的值域
（1） 
（2） , 
已知函数
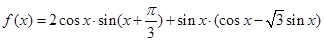
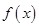（1）求函数的最小正周期和单调递减区间；
（2）在中，分别是角A、B、C的对边，若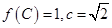,求 面积的最大值．
若cos（2π-α）=
2
2
3
，且α∈（-
π
2
，0），则sin（π+α）=（　　）
A．-
1
3
B．-
2
3
C．
1
3
D．
2
3
求值化简：
（Ⅰ）（
32
×
3
）6+（
2
2
）
4
3
+lg500-lg0.5
（Ⅱ）
sin(π-2α)•cos(π-α)
1+sin(
π
2
+2α)
．
已知f（α）=
sin(180°-α)sin(270°-α)tan(180°-α)
sin(90°+α)tan(180°+α)tan(360°-α)
，则f（-
31π
6
）的值为______．
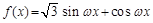已知函数(ω＞0)的图象与直线y＝－2的两个相邻公共点之间的距离等于π，则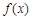的单调递减区间是（     ）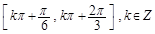
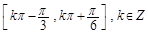
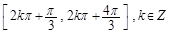
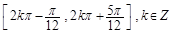
A．B．
C．D．
化简：
（10分）已知=化简.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网