题目内容
若对一切非零实数,已知函数y=f(x)(x≠0),满足f(xy)=f(x)+f(y),
(1)求f(1),f(-1),
(2)判断函数y=f(x)的奇偶性;
(3)若y=f(x),在(0,+∞)上是增函数,且满足y=f(x)+f(x-
)≤0,求x的取值范围.
(1)求f(1),f(-1),
(2)判断函数y=f(x)的奇偶性;
(3)若y=f(x),在(0,+∞)上是增函数,且满足y=f(x)+f(x-
| 1 | 2 |
分析:(1)令x=y=1,可求得f(1),再令x=-1,y=-1可求得f(-1);
(2)令y=-1,代入f(xy)=f(x)+f(y),结合(1)的结论,即可判断函数y=f(x)的奇偶性;
(3)依题意,将已知关系式逆用f(xy)=f(x)+f(y),结合(2)中函数y=f(x)的奇偶性与在(0,+∞)上是增函数,即可求得x的取值范围.
(2)令y=-1,代入f(xy)=f(x)+f(y),结合(1)的结论,即可判断函数y=f(x)的奇偶性;
(3)依题意,将已知关系式逆用f(xy)=f(x)+f(y),结合(2)中函数y=f(x)的奇偶性与在(0,+∞)上是增函数,即可求得x的取值范围.
解答:解:(1)∵函数y=f(x)(x≠0),满足f(xy)=f(x)+f(y),
∴令x=y=1得:f(1)=2f(1),故f(1)=0;
再令x=y=-1得:f(1)=2f(-1)=0,故f(-1)=0;
(2)令y=-1,则f(-x)=f(x)+f(-1)=f(x)
故f(x)是偶函数;
(3)∵f(x)+f(x-
)=f[x(x-
)]≤0,偶函数y=f(x)在(0,+∞)上是增函数,f(-1)=f(1)=0,
∴|x(x-
)|≤1,
∴-1≤x(x-
)≤1,
∴
,①的解集为R,
解②得
≤x≤
,又x≠0.
∴x的取值范围为:[
,0)∪(0,
].
∴令x=y=1得:f(1)=2f(1),故f(1)=0;
再令x=y=-1得:f(1)=2f(-1)=0,故f(-1)=0;
(2)令y=-1,则f(-x)=f(x)+f(-1)=f(x)
故f(x)是偶函数;
(3)∵f(x)+f(x-
| 1 |
| 2 |
| 1 |
| 2 |
∴|x(x-
| 1 |
| 2 |
∴-1≤x(x-
| 1 |
| 2 |
∴
|
解②得
1-
| ||
| 4 |
1+
| ||
| 4 |
∴x的取值范围为:[
1-
| ||
| 4 |
1+
| ||
| 4 |
点评:本题考查抽象函数及其应用,考查函数奇偶性与单调性的综合,突出考查赋值法的应用,考查推理与运算能力,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)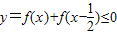 ,求x的取值范围.
,求x的取值范围.