Question

考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
A．（几何证明选做题） 如图，圆O的直径AB=10，弦DE⊥AB于点H，HB=2．则DE=

8

．
B．（坐标系与参数方程选做题）已知直线C₁

x=1+tcosα y=tsinα

（t为参数），C₂

x=cosθ y=sinθ

（θ为参数），当α=

π

3

时，C₁与C₂的交点坐标为

(1，0)；(

1

2

，-

3

2

)

．
C．（不等式选做题）若不等式|2a-1|≤|x+

1

x

|对一切非零实数a恒成立，则实数a的取值范围

[-

1

2

，

3

2

]

．

Answer 1

分析：A：连接OD．根据垂径定理和勾股定理求解．
B：先写出C₁的普通方程和C₂的普通方程为x²+y²=1．联立方程组即可解得C₁与C₂的交点；
C：由题意得不等式|2a-1|≤|x+

1

x

|对一切非零实数x均成立，由于|x+

1

x

|的最小值等于2，可得关于a的不等关系，从而求得答案．

解答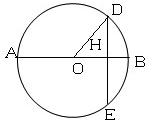：解：A：连接OD，圆的直径为10，HB=2
那么，OD=5，OH=OB-HB=5-2=3，
直角三角形ODH中，根据勾股定理可得：
DH²+OH²=OD²，即DH²+3²=5²，
解得DH=4，
∴DE=2DH=8．
故答案为：8．

B：当α=

π

3

时，C₁的普通方程为y=

3

(x-1)，C₂的普通方程为x²+y²=1．
联立方程组

y= 3 (x-1) x2+y2=1

，
解得C₁与C₂的交点为（1，0）(

1

2

，-

3

2

)．
故答案为：(1，0)；(

1

2

，-

3

2

)．

C：∵不等式|2a-1|≤|x+

1

x

|对于一切非零实数x均成立，
由于|x+

1

x

|=|x|+

1

|x|

≥2，故|x+

1

x

|的最小值等于2，
∴|2a-1|≤2，
∴-

1

2

≤a≤

3

2

，
故答案为：[-

1

2

，

3

2

]．

点评：本题主要考查与圆有关的比例线段，以及圆的参数方程和直线的参数方程，以及绝对值不等式等基础知识，是一道综合题，属于中档题．（C）小题考查查绝对值不等式，基本不等式的应用以及函数的恒成立问题，求出|x+

1

x

|的最小值是解题的关键．