题目内容
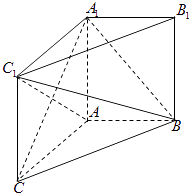
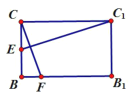
【题目】如图,在直三棱柱![]() 中,底面
中,底面![]() 为等边三角形,
为等边三角形, ![]() .
.
(Ⅰ)求三棱锥![]() 的体积;
的体积;
(Ⅱ)在线段![]() 上寻找一点
上寻找一点![]() ,使得
,使得![]() ,请说明作法和理由.
,请说明作法和理由.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】试题分析:(1)取BC中点E连结AE,三棱锥C1﹣CB1A的体积![]() ,由此能求出结果.(2)在矩形BB1C1C中,连结EC1,推导出Rt△C1CE∽Rt△CBF,从而CF⊥EC1,再求出AE⊥CF,由此得到在BB1上取F,使得
,由此能求出结果.(2)在矩形BB1C1C中,连结EC1,推导出Rt△C1CE∽Rt△CBF,从而CF⊥EC1,再求出AE⊥CF,由此得到在BB1上取F,使得![]() ,连结CF,CF即为所求直线.
,连结CF,CF即为所求直线.
解析:(1)取![]() 中点
中点![]() 连结
连结![]() .在等边三角形
.在等边三角形![]() 中,
中, ![]() ,
,
又∵在直三棱柱![]() 中,侧面
中,侧面![]() 面
面![]() ,
,
面![]() 面
面![]() ,∴
,∴![]() 面
面![]() ,
,
∴![]() 为三棱锥
为三棱锥![]() 的高,又∵
的高,又∵![]() ,∴
,∴![]() ,
,
又∵底面![]() 为直角三角形,∴
为直角三角形,∴![]() ,
,
∴三棱锥![]() 的体积
的体积![]()
![]()
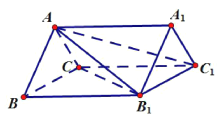
(2)作法:在![]() 上取
上取![]() ,使得
,使得![]() ,连结
,连结![]() ,
, ![]() 即为所求直线.
即为所求直线.
证明:如图,在矩形![]() 中,连结
中,连结![]() ,
,
∵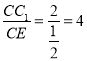 ,
, 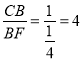 ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵![]() 面
面![]() ,而
,而![]() 面
面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 面
面![]() ,
,
又∵![]() 面
面![]() ,∴
,∴![]() .
.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目