题目内容
已知曲线C:y=
x3-x2-4x+1,直线l:x+y+2k-1=0,当x∈[-3,3]时,直线l 恒在曲线C的上方,则实数k的取值范围是( )
| 1 |
| 3 |
A.k>-
| B.k<-
| C.K<
| D.K>
|
命题等价于x在(-3,3)内,
(-x-2k+1)-(
x3-x2-4x+1)>0恒成立
即k<-
x3+
x2+
x,
设y=-
x3+
x2+
x,
y'=-
x2+x+
=
(3-x)(1+x)
所以函数y=-
x3+
x2+
x,
在[-3,-1)内y递减,(-1,3]内递增
所以x=-1,y取最小值-
所以k<-
故选B.
(-x-2k+1)-(
| 1 |
| 3 |
即k<-
| 1 |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
设y=-
| 1 |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
y'=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
所以函数y=-
| 1 |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
在[-3,-1)内y递减,(-1,3]内递增
所以x=-1,y取最小值-
| 5 |
| 6 |
所以k<-
| 5 |
| 6 |
故选B.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 (2006•南京二模)如图,已知曲线C:
(2006•南京二模)如图,已知曲线C:
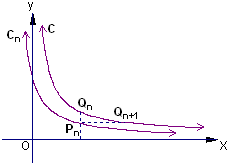 如图,已知曲线C:
如图,已知曲线C: 如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.
如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.