题目内容
对数函数f(x)的图象过P(8,3),则f(
)= .
| 1 |
| 2 |
考点:对数函数的单调性与特殊点
专题:函数的性质及应用
分析:设对数函数f(x)=logax,由f(x)的图象过P(8,3),求得a的值,可得可得f(
)的值.
| 1 |
| 2 |
解答:
解:设对数函数f(x)=logax,∵f(x)的图象过P(8,3),可得loga8=3,
求得a=2,可得f(
)=log2
=-1,
故答案为:-1.
求得a=2,可得f(
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:-1.
点评:本题主要考查对数函数的单调性和特殊点,用待定系数法求函数的解析式、求函数的值,属于基础题.

练习册系列答案
相关题目
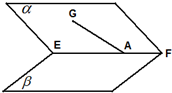 平面角为锐角的二面角α-EF-β,A∈EF,AG?α,∠GAE=45°,若AG与β所成角为30°,则二面角α-EF-β的大小是
平面角为锐角的二面角α-EF-β,A∈EF,AG?α,∠GAE=45°,若AG与β所成角为30°,则二面角α-EF-β的大小是 如图,F1、F2是双曲线
如图,F1、F2是双曲线