题目内容
已知函数
.
（1）若不等式
的解集为空集，求
的范围；
（2）若
，且
，求证：
.
（1）
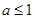；（2）证明略．
解析试题分析：
解题思路：（1）利用
求不等式左边的最小值，在得出的范围即可；（2）用分析法进行证明即可.
规律总结：1.在求含两个绝对值的不等式的最值时，往往要利用
，并且要注意等号成立的条件；（2）证明不等式的基本.方法有：综合法、分析法，或两者结合使用.
注意：由不等式的解集为空集得到的应是
，学生往往会出现错误.
试题解析：（1）
（2）要证，只需证
，只需证
而
，
从而原不等式成立. .
考点1.绝对值不等式；2.分析法.
练习册系列答案
相关题目
(
+
+
).
的解集是
．
，求
的取值范围；
，求不等式
的解集．
，
，记
的解集为M，
的解集为N.
时，证明：
.
，求证
；
，求证：
.
,
=
,anan+1<0(n≥1,n∈N+),数列{bn}满足:bn=
-
(n≥1,n∈N+).
，则x＋y＋z＝________.