题目内容
3.已知函数$f(x)=\frac{x^3}{cosx}$的定义域为$({-\frac{π}{2},\frac{π}{2}})$,当$|{x_i}|<\frac{π}{2}$(i=1,2,3)时,若x1+x2>0,x2+x3>0,x1+x3>0,则有f(x1)+f(x2)+f(x3)的值( )| A. | 恒小于零 | B. | 恒等于零 | ||
| C. | 恒大于零 | D. | 可能大于零,也可能小于零 |
分析 分析出函数$f(x)=\frac{x^3}{cosx}$的奇偶性和单调性,进而结合x1+x2>0,x2+x3>0,x1+x3>0,可得f(x1)+f(x2)+f(x3)的值恒为正.
解答 解:函数$f(x)=\frac{x^3}{cosx}$的定义域$({-\frac{π}{2},\frac{π}{2}})$关于原点对称,
且满足f(-x)=-f(x),故函数f(x)为奇函数,
又由$f′(x)=\frac{3{x}^{2}cosx+{x}^{3}sinx}{co{s}^{2}x}$>0,在x∈$(0,\frac{π}{2})$时恒成立,
故x∈$(0,\frac{π}{2})$时,函数为增函数,
进而可得x∈$({-\frac{π}{2},\frac{π}{2}})$时,函数为增函数,
若x1+x2>0,x2+x3>0,x1+x3>0,
则x1>-x2,x2>-x3,x3>-x1,
则f(x1)>f(-x2)=-f(x2),f(x2)>f(-x3)=-f(x3),f(x3>f(-x1)=-f(x1),
即f(x1)+f(x2)>0,f(x2)+f(x3)>0,f(x1)+f(x3)>0,
故2[f(x1)+f(x2)+f(x3)]>0,
即f(x1)+f(x2)+f(x3)的值恒大于零,
故选:C.
点评 本题考查的知识点是函数恒成立问题,利用导数研究函数的单调性,函数的奇偶性,难度中档.

练习册系列答案
相关题目
13.函数$f(x)=\frac{1}{{{3^{x-1}}}}-3$是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数也是偶函数 | D. | 既不是奇函数也不是偶函数 |
11.已知两曲线f(x)=$\frac{1}{2}$x2+ax与g(x)=2a2lnx+b有公共点,且在该点处有相同的切线,则a∈(0,+∞)时,实数b的最大值是( )
| A. | e${\;}^{\frac{1}{2}}$ | B. | 2e${\;}^{\frac{1}{2}}$ | C. | e${\;}^{\frac{2}{3}}$ | D. | $\frac{3}{2}$e${\;}^{\frac{2}{3}}$ |
8.已知集合A={x|x2-4x<0},B={x|x<a},若A⊆B,则实数a的取值范围是( )
| A. | (0,4] | B. | (-∞,4) | C. | [4,+∞) | D. | (4,+∞) |
12.为了得到函数$y=3sin(2x+\frac{π}{5})$的图象,只需把y=3sin2x上的所有的点( )
| A. | 向左平行移动$\frac{π}{10}$长度单位 | B. | 向右平行移动$\frac{π}{10}$长度单位 | ||
| C. | 向右平行移动$\frac{π}{5}$长度单位 | D. | 向左平行移动$\frac{π}{5}$长度单位 |
1.执行如图所示的程序框图,若输入t的值为6,则输出的s的值为( )
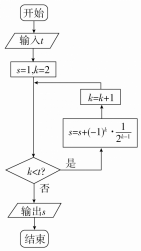

| A. | $\frac{9}{16}$ | B. | $\frac{5}{4}$ | C. | $\frac{21}{16}$ | D. | $\frac{11}{8}$ |
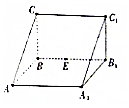 如图,直三棱柱ABC-A1B1C1中,AA1=2,AB=BC=1,∠ABC=90°,外接球的球心为O,点E是侧棱BB1上的一个动点.有下列判断:
如图,直三棱柱ABC-A1B1C1中,AA1=2,AB=BC=1,∠ABC=90°,外接球的球心为O,点E是侧棱BB1上的一个动点.有下列判断: