题目内容
17.某种型号电子元件的寿命X(以h计)具有概率密度,f(x)=$\left\{\begin{array}{l}{\frac{1500}{{x}^{2}},x>1500}\\{0,其他}\end{array}\right.$,现有一大批此种元件(设各元件损坏与否相互独立),任取5只,问其中至少有2只寿命大于3000h的概率是多少?分析 由题意,P(X>3000)=${∫}_{3000}^{+∞}\frac{1500}{{x}^{2}}dx$=$\frac{1}{3}$.设Y为寿命大于3000h的只数,利用P(Y≥2)=1-P(Y=0)-P(Y=1),可得结论.
解答 解:由题意,P(X>3000)=${∫}_{3000}^{+∞}\frac{1500}{{x}^{2}}dx$=$\frac{1}{3}$.
设Y为寿命大于3000h的只数,则P(Y≥2)=1-P(Y=0)-P(Y=1)=1-$(\frac{2}{3})^{5}$-${C}_{5}^{1}•\frac{1}{3}•(\frac{2}{3})^{4}$=$\frac{131}{243}$.
点评 本题考查概率知识的运用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
8.下列结论正确的个数是( )
①若x>0,则x>sinx恒成立;
②命题“?x>0,x-lnx>0”的否定是“?x>0,x0-lnx0≤0”;
③“命题p∨q为真”是“命题p∧q为真”的充分不必要条件.
①若x>0,则x>sinx恒成立;
②命题“?x>0,x-lnx>0”的否定是“?x>0,x0-lnx0≤0”;
③“命题p∨q为真”是“命题p∧q为真”的充分不必要条件.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.如图,在三棱锥V-ABC,VA=VC,VB⊥AC,则AB与BC的大小关系是( )
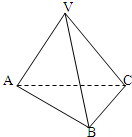

| A. | AB>BC | B. | AB=BC | C. | AB<BC | D. | 无法确定 |