如图.在三棱锥V-ABC.VA=VC.VB⊥AC.则AB与BC的大小关系是( )A．AB＞BCB．AB=BCC．AB＜BCD．无法确定题目和参考答案——青夏教育精英家教网—

题目内容

6．如图，在三棱锥V-ABC，VA=VC，VB⊥AC，则AB与BC的大小关系是（　　）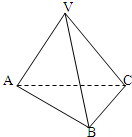

A．

AB＞BC

B．

AB=BC

C．

AB＜BC

D．

无法确定

分析取AC的中点D，连接VD，BD，根据线面垂直的判定定理，可得AC⊥平面VBD，进而AC⊥BD，故△ABC为等腰三角形，AB=BC．

解答解：取AC的中点D，连接VD，BD，如图所示：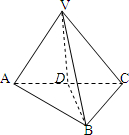

∵VA=VC，
∴VD⊥AC，
又∵VB⊥AC，VB，VD?平面VBD，VB∩VD=V，
∴AC⊥平面VBD，
又∵BD?平面VBD，
∴AC⊥BD，
故△ABC为等腰三角形，AB=BC，
故选：B．

点评本题考查的知识点是线面垂直的判定与性质，等腰三角形的性质及判定，难度中档．

练习册系列答案

小学语文词语手册吉林教育出版社系列答案

17．某种型号电子元件的寿命X（以h计）具有概率密度，f（x）=$\left\{\begin{array}{l}{\frac{1500}{{x}^{2}}，x＞1500}\\{0，其他}\end{array}\right.$，现有一大批此种元件（设各元件损坏与否相互独立），任取5只，问其中至少有2只寿命大于3000h的概率是多少？

14．已知函数f（x）=$\frac{3x}{a}$-2x²+lnx（a∈R且a≠0），当a=3时，求函数的单调区间．

1．（1）已知函数y=$\frac{1}{{x}^{2}-mx+1}$的定义域为R，求实数m的取值范围；
（2）若关于x的不等式-x²-ax+a-3≤0在[-2，2]上恒成立．求实数a的取值范围．

11．已知等比数列{a_n}中，a₂a₈=4，那么a₅=（　　）

18．设函数f（x）=x²-x+b，已知log₂f（a）=2，且f（log₂a）=b（a＞0且a≠1），求a、b的值．

15．容器A中有m升水，将容器A中的水缓慢注入容器B中，t分钟后容器A中剩余水量y（单位：升）符合函数关系式y=m•3^-at（a为正常数）．假设经过5分钟后，容器A中的水量和容器B中的水量相等，再经过n分钟，容器A中的水只剩$\frac{m}{8}$，求n的值．

16．函数y=2sin（x-$\frac{π}{3}$）（$\frac{π}{6}$≤x≤$\frac{2π}{3}$）的最小值是（　　）

试题分类