题目内容
1.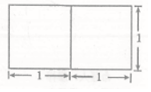 一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在同一个球面上,则该球的内接正方体的表面积为( )
一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在同一个球面上,则该球的内接正方体的表面积为( )| A. | $\frac{19}{6}$ | B. | $\frac{38}{3}$ | C. | $\frac{57}{8}$ | D. | $\frac{19}{3}$ |
分析 由已知中底面是正三角形的三棱柱的正视图,求出三棱柱的底面边长和高,从而求出它外接球的半径,再求球内接正方体的棱长,即可求出其表面积.
解答 解:由已知中的三棱柱正视图可得:
三棱柱的底面边长为2,高为1
则三棱柱的底面外接圆半径为
r=$\frac{2\sqrt{3}}{3}$,
球心到底面的距离为
d=$\frac{1}{2}$;
则球的半径为
R=$\sqrt{{r}^{2}{+d}^{2}}$=$\sqrt{\frac{19}{12}}$;
∴该球的内接正方体对角线长是
2R=2$\sqrt{\frac{19}{12}}$=$\sqrt{3}$a,
∴a=2$\sqrt{\frac{19}{36}}$=$\frac{\sqrt{19}}{3}$;
∴内接正方体的表面积为:
S=6a2=6×$\frac{19}{9}$=$\frac{38}{3}$.
故选:D.
点评 本题考查了球与三棱柱、正方体的关系与应用问题,根据条件确定三棱柱的底面边长和高,根据棱柱的底面外接圆半径,球心距,球半径求出球半径是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.为了得到函数$y=3sin({\frac{1}{2}x-\frac{π}{5}})$,x∈R的图象,只需把函数$y=3sin({\frac{1}{2}x+\frac{π}{5}})$的图象上所有点( )
| A. | 向左平行移动$\frac{2π}{5}$个单位长度 | B. | 向右平行移动$\frac{2π}{5}$个单位长度 | ||
| C. | 向左平行移动$\frac{4π}{5}$个单位长度 | D. | 向右平行移动$\frac{4π}{5}$个单位长度 |
12.已知等差数列{an}满足a1+a2=-1,a3=4,则a4+a5=( )
| A. | 17 | B. | 16 | C. | 15 | D. | 14 |
9.一个三棱锥的三视图如图(图中小正方形的边长为1),则这个三棱锥的体积是( )
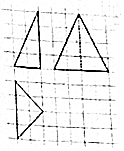

| A. | $\frac{32}{3}$ | B. | 8 | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
16.定义运算$|{\begin{array}{l}a&b\\ c&d\end{array}}|=ad-bc$,则符合条件$|{\begin{array}{l}z&{1+i}\\{-i}&{2i}\end{array}}|=0$的复数z的共轭复数$\overline z$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.通过$\widehat{{e}_{1}}$,$\widehat{{e}_{2}}$,…,$\widehat{{e}_{n}}$来判断模拟型拟合的效果,判断原始数据中是否存在可疑数据,这种分工称为( )
| A. | 回归分析 | B. | 独立性检验分析 | C. | 残差分析 | D. | 散点图分析 |
11.将函数y=sin(x-$\frac{π}{12}$)图象上的点P($\frac{π}{4}$,t)向左平移s(s>0)个单位,得到点P′,若P′位于函数y=sin2x的图象上,则( )
| A. | t=$\frac{1}{2}$,s的最小值为$\frac{π}{6}$ | B. | t=$\frac{\sqrt{3}}{2}$,s的最小值为$\frac{π}{6}$ | ||
| C. | t=$\frac{1}{2}$,s的最小值为$\frac{π}{12}$ | D. | t=$\frac{\sqrt{3}}{2}$,s的最小值为$\frac{π}{12}$ |