题目内容
已知某几何体的俯视图是如图7所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.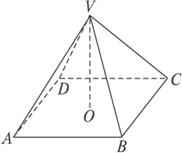
图7
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
解:由三视图可知该几何体是一个底面边长分别为6、8的矩形,高为4的四棱锥.设底面矩形为ABCD.如图8所示,

图8
AB=8,BC=6,高VO=4.
(1)V=![]() ×(8×6)×4=64.
×(8×6)×4=64.
(2)设四棱锥侧面VAD、VBC是全等的等腰三角形,侧面VAB、VCD也是全等的等腰三角形,
在△VBC中,BC边上的高为h1=![]() =
=![]() =
=![]() ,
,
在△VAB中,AB边上的高为h2=![]() =
=![]() =5.
=5.
所以此几何体的侧面积S=2(![]() ×6×
×6×![]() +
+![]() ×8×5)=40+24
×8×5)=40+24![]() .
.
点评:高考试题中对面积和体积的考查有三种方式:一是给出三视图,求其面积或体积;二是与组合体有关的面积和体积的计算;三是在解答题中,作为最后一问.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
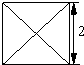 已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其全面积是( )
已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其全面积是( )| A、8 | ||
| B、12 | ||
C、4(1+
| ||
D、4
|
 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形. 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为4、高为3的等腰三角形.则该几何体的侧面积为( )
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为4、高为3的等腰三角形.则该几何体的侧面积为( ) 已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形,则该几何体的体积为
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形,则该几何体的体积为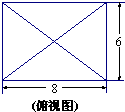 已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图是一个底边为6,高为4的等腰三角形,求该几何体的表面积.
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图是一个底边为6,高为4的等腰三角形,求该几何体的表面积.