题目内容
 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
分析:由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h1的等腰三角形,左、右侧面均为底边长为6、高为h2的等腰三角形,分析出图形之后,再利用公式求解即可.
解答: 解:由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h1的等腰三角形,左、右侧面均为底边长为6、高为h2的等腰三角形,如图所示.
解:由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h1的等腰三角形,左、右侧面均为底边长为6、高为h2的等腰三角形,如图所示.
(1)几何体的体积为
V=
•S矩形•h=
×6×8×4=64.
(2)正侧面及相对侧面底边上的高为:
h1=
=5.
左、右侧面的底边上的高为:
h2=
=4
.
故几何体的侧面面积为:
S=2×(
×8×5+
×6×4
)
=40+24
.
 解:由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h1的等腰三角形,左、右侧面均为底边长为6、高为h2的等腰三角形,如图所示.
解:由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h1的等腰三角形,左、右侧面均为底边长为6、高为h2的等腰三角形,如图所示.(1)几何体的体积为
V=
| 1 |
| 3 |
| 1 |
| 3 |
(2)正侧面及相对侧面底边上的高为:
h1=
| 42+32 |
左、右侧面的底边上的高为:
h2=
| 42+42 |
| 2 |
故几何体的侧面面积为:
S=2×(
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
=40+24
| 2 |
点评:本题考查了学生的空间想象能力,图形确定后,本题就容易了,是中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
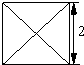 已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其全面积是( )
已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其全面积是( )| A、8 | ||
| B、12 | ||
C、4(1+
| ||
D、4
|
 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为4、高为3的等腰三角形.则该几何体的侧面积为( )
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为4、高为3的等腰三角形.则该几何体的侧面积为( ) 已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形,则该几何体的体积为
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形,则该几何体的体积为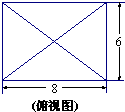 已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图是一个底边为6,高为4的等腰三角形,求该几何体的表面积.
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图是一个底边为6,高为4的等腰三角形,求该几何体的表面积.