题目内容
已知f（x）=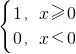
则不等式xf（x）+x≤2的解集是________．
{x|x≤1}
分析：由题意，不等式求解必须分类讨论，分x≥0、x＜0时解答，最后求并集．
解答：x≥0时，f（x）=1，
xf（x）+x≤2?x≤1，∴0≤x≤1；
当x＜0时，f（x）=0，
xf（x）+x≤2?x≤2，∴x＜0．综上x≤1．
故答案为：{x|x≤1}
点评：本题利用分类讨论的数学思想解答不等式，考查学生发现问题解决问题的能力，是基础题．
分析：由题意，不等式求解必须分类讨论，分x≥0、x＜0时解答，最后求并集．
解答：x≥0时，f（x）=1，
xf（x）+x≤2?x≤1，∴0≤x≤1；
当x＜0时，f（x）=0，
xf（x）+x≤2?x≤2，∴x＜0．综上x≤1．
故答案为：{x|x≤1}
点评：本题利用分类讨论的数学思想解答不等式，考查学生发现问题解决问题的能力，是基础题．
练习册系列答案
相关题目
已知f（x）=alnx+
x2（a＞0），若对任意两个不等的正实数x1，x2，都有
＞2恒成立，则a的取值范围是（ ）
| 1 |
| 2 |
| f(x1)-f(x2) |
| x1-x2 |
| A、（0，1] |
| B、（1，+∞） |
| C、（0，1） |
| D、[1，+∞） |