Question

已知双曲线

x2

a2

-

y2

b2

=1(b＞a＞0)的两条渐近线的夹角为

π

3

，则双曲线的离心率为

2

．

Answer 1

分析：由双曲线

x2

a2

-

y2

b2

=1(b＞a＞0)的两条渐近线的夹角为

π

3

，可得

b

a

=

3

，进而可得离心率．

解答：解：∵b＞a＞0，∴

b

a

＞1．如图所示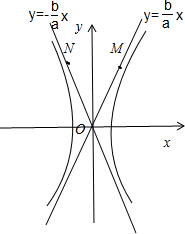，分别在两条渐近线上取点M，N．
∵双曲线

x2

a2

-

y2

b2

=1的两条渐近线的夹角为

π

3

，且b＞a＞1．
∴

b

a

＞1，
∴应是∠MON=

π

3

．而∠MOx＞

π

4

．
∴∠MOx=

π

2

-

1

2

×

π

3

=

π

3

．
∴

b

a

=tan∠MOx=tan

π

3

=

3

．
∴e=

c

a

=

1+ b2 a2

=2．
故答案为2．

点评：本题考查了双曲线的渐近线的性质、离心率的计算公式等基础知识与基本方法，属于基础题．