题目内容
已知函数f（x）连续，且f（x）=x-
f（x）dx，求函数f（x）．
| ∫ | 1 0 |
考点：定积分
专题：计算题
分析：设u=
f(x)dx，代入f（x）=x-
f（x）dx后两边取对x的积分，得到关于u的等式，转换为f（x）的解析式得答案．
| ∫ | 1 0 |
| ∫ | 1 0 |
解答：
解：设u=
f(x)dx，则
f（x）=x-u，两边取对x的积分，得
f(x)dx
(x-u)dx，
即u=
(x-u)dx，
∴u=(
-ux)
=
-u，
∴u=
．
即f（x）=x-
．
| ∫ | 1 0 |
f（x）=x-u，两边取对x的积分，得
| ∫ | 1 0 |
| =∫ | 1 0 |
即u=
| ∫ | 1 0 |
∴u=(
| x2 |
| 2 |
| | | 1 0 |
| 1 |
| 2 |
∴u=
| 1 |
| 4 |
即f（x）=x-
| 1 |
| 4 |
点评：本题考查了定积分，训练了换元法在求解定积分中的应用，是基础题．
练习册系列答案
相关题目
不等式x2-2x-3＜0的解集是（ ）
| A、{x|x＜-1} |
| B、{x|x＞3} |
| C、{x|-1＜x＜3} |
| D、{x|x＜-1或x＞3} |
设集合A={x|
＞1}，B={y|y=2x}，x∈[-1，0]，则A∪B=（ ）
| 1 |
| x |
| A、（-∞，1] | B、（0，1） |
| C、（0，1] | D、∅ |
如图，正方体ABCD-A1B1C1D1中，AB=2，则三棱锥A-A1B1C的体积是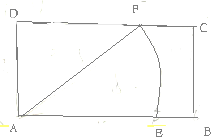
如图，矩形ABCD两邻边长分别为AB=6，AD=3，以A为圆心，5为半径画圆交AB于E，交CD于F，定义点集I={P|AP≤5}