Question

（09年海淀区期末理）（14分）

  如果正数数列满足：对任意的正数M，都存在正整数则称数列是一个无界正数列。

（I）若分别判断数列、是否为无界正数列，并说明理由；

（II）若成立。

（III）若数列是单调递增的无界正数列，求证：存在正整数m，使得

       

Answer 1

解析：（I）不是无界正数列，理由如下：…………1分

       取M=5，显然…………2分

       是无界正数列，理由如下：…………3分

       对任意的正数M，取

       所以是无界正数列…………4分，

   （II）存在满足题意的正整数k，理由如下：

       当时，

       因为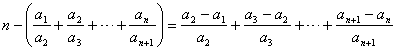

      

       读取成立。…………9分

       注：k取大于或等于3的整数即可。

   （III）证明：因为数列是单调递增的正数列，

       所以

      

       即

       因为是无界正数列，取，由定义知存在正整数

       所以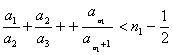

       由定义可知是无穷数列，考察数列显然这仍是一个单调递增的无界正数列，同上理由可知存在正整数，使得

   

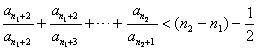
重复上述操作，直到确定相应的正整数

       则

      

       即存在正整数成立。……14分

       说 明：其他正确解法按相应步骤给分。