题目内容
已知双曲线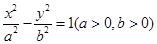 的两条渐近线均和圆
的两条渐近线均和圆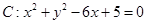 相切,且双曲线的右焦点为圆
相切,且双曲线的右焦点为圆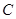 的圆心,则该双曲线的方程为( )
的圆心,则该双曲线的方程为( )
A.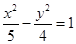 | B.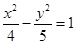 | C.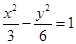 | D.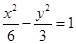 |
A
解析试题分析:圆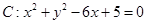 化为
化为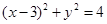 ,其圆心为
,其圆心为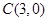 ,半径
,半径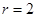 ,由题意知,双曲线的右焦点为
,由题意知,双曲线的右焦点为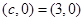 ,另双曲线的的一条渐近线为
,另双曲线的的一条渐近线为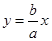 ,即
,即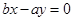 ,由于渐近线均和圆相切,则
,由于渐近线均和圆相切,则 ,化为
,化为 ,结合
,结合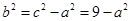 得
得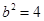 ,
,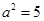 ,所以双曲线的方程
,所以双曲线的方程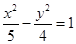 。故选A。
。故选A。
考点:双曲线的性质
点评:解决平面几何的题目,首先是画图。当题目出现曲线的方程时,假如不是标准形式,则需要将其变成标准形式。

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
若双曲线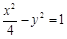 的渐近线与圆
的渐近线与圆 (
(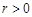 )相切,则
)相切,则
| A.5 | B.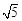 | C.2 | D. |
过双曲线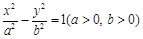 左焦点
左焦点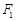 的直线与以右焦点
的直线与以右焦点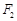 为圆心、
为圆心、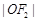 为半径的圆相切于A点,且
为半径的圆相切于A点,且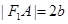 ,则双曲线的离心率为
,则双曲线的离心率为
A.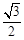 | B.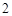 | C.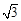 | D.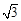 |
抛物线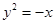 的焦点坐标为( )
的焦点坐标为( )
A.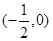 | B.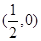 | C.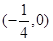 | D.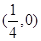 |
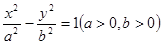 的左右焦点分别是
的左右焦点分别是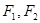 ,设
,设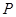 是双曲线右支上一点,
是双曲线右支上一点,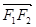 在
在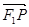 上投影的大小恰好为
上投影的大小恰好为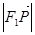 ,且它们的夹角为
,且它们的夹角为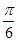 ,则双曲线的离心率为( )
,则双曲线的离心率为( )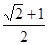
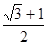
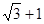
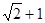
 (
(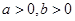 )的右焦点
)的右焦点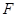 作圆
作圆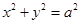 的切线
的切线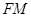 ,交
,交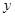 轴于点
轴于点 ,切圆于点
,切圆于点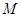 ,若
,若 ,则双曲线的离心率是( )
,则双曲线的离心率是( )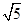


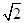
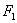 、
、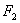 是一对相关曲线的焦点,
是一对相关曲线的焦点,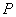 是它们在第一象限的交点,当
是它们在第一象限的交点,当 时,这一对相关曲线中双曲线的离心率是( )
时,这一对相关曲线中双曲线的离心率是( )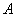 .
.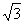
 .
.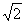
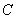 .
.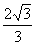
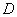 .
.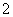
 为C的实轴长的2倍,则双曲线C的离心率为( )
为C的实轴长的2倍,则双曲线C的离心率为( )
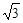
 和
和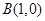 ,动点
,动点 在直线
在直线 上移动,椭圆
上移动,椭圆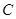 以
以 为焦点且经过点
为焦点且经过点 ,记椭圆
,记椭圆 ,则函数
,则函数 的大致图像是( )
的大致图像是( )