题目内容
已知双曲线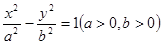 的左右焦点分别是
的左右焦点分别是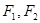 ,设
,设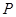 是双曲线右支上一点,
是双曲线右支上一点,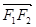 在
在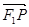 上投影的大小恰好为
上投影的大小恰好为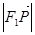 ,且它们的夹角为
,且它们的夹角为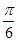 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.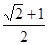 | B.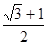 | C.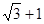 | D.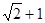 |
C
解析试题分析:解:∵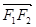 在
在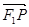 上的投影的大小恰好为
上的投影的大小恰好为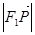 ∴PF1⊥PF2,且它们的夹角为
∴PF1⊥PF2,且它们的夹角为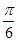 ,∴∠PF 1F 2=
,∴∠PF 1F 2=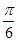
∴在直角三角形PF1F2中,F1F2=2c,∴PF2=c,PF1= c,又根据双曲线的定义得:PF1-PF2=2a,∴
c,又根据双曲线的定义得:PF1-PF2=2a,∴ c-c=2a,∴
c-c=2a,∴
c:a=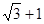 ,e=
,e=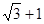 故选C.
故选C.
考点:双曲线的简单性质.
点评:本题主要考查了双曲线的简单性质.考查了学生综合分析问题和运算的能力.解答关键是通过解三角形求得a,c的关系从而求出离心率.

练习册系列答案
相关题目
将两个顶点在抛物线 上,另一个顶点
上,另一个顶点 ,这样的正三角形有( )
,这样的正三角形有( )
| A.0个 | B.2个 | C.4个 | D.1个 |
极坐标方程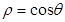 和参数方程
和参数方程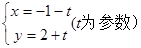 所表示的图形分别是( )
所表示的图形分别是( )
| A.直线,直线 | B.直线,圆 |
| C.圆,圆 | D.圆,直线 |
设F为抛物线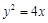 的焦点,
的焦点,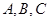 为抛物线上不同的三点,点
为抛物线上不同的三点,点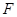 是△ABC的重心,
是△ABC的重心, 为坐标原点,△
为坐标原点,△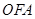 、△
、△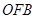 、△
、△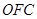 的面积分别为
的面积分别为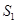 、
、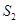 、
、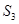 ,则
,则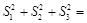 ( )
( )
| A.9 | B.6 | C.3 | D.2 |
已知抛物线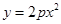 (p>0)的准线与圆
(p>0)的准线与圆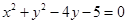 相切,则p的值为( )
相切,则p的值为( )
| A.10 | B.6 | C.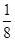 | D.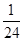 |
顶点在原点,经过圆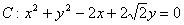 的圆心且准线与
的圆心且准线与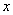 轴垂直的抛物线方程为
轴垂直的抛物线方程为
A.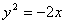 | B.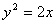 |
C.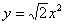 | D.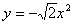 |
已知双曲线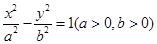 的两条渐近线均和圆
的两条渐近线均和圆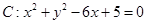 相切,且双曲线的右焦点为圆
相切,且双曲线的右焦点为圆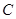 的圆心,则该双曲线的方程为( )
的圆心,则该双曲线的方程为( )
A.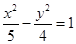 | B.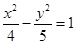 | C.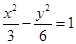 | D.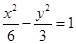 |
已知椭圆 上的一点
上的一点 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为 ,则
,则 到另一焦点距离为
到另一焦点距离为
A. | B. | C. | D. |
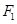 、
、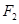 分别为双曲线
分别为双曲线 的左、右焦点.若在双曲线右支上存在点
的左、右焦点.若在双曲线右支上存在点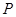 ,满足
,满足 ,且
,且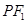 的距离等于双曲线的实轴长,则该双曲线的离心率为( )
的距离等于双曲线的实轴长,则该双曲线的离心率为( )