题目内容
19.函数y=sinxcosx+sinx+cosx(x∈R)的最大值是$\frac{1}{2}+\sqrt{2}$.分析 利用换元法,转化为二次函数问题,利用二次函数性质即可求最大值.
解答 解:函数y=sinxcosx+sinx+cosx.
令sinx+cosx=t,
由于sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)=t,
∴$-\sqrt{2}≤$t$≤\sqrt{2}$
则sinxcosx=$\frac{{t}^{2}-1}{2}$.
那么:函数y 转化为g(t)=$\frac{1}{2}{t}^{2}+t-\frac{1}{2}$,($-\sqrt{2}≤$t$≤\sqrt{2}$)
可知g(t)开口向上,对称轴x=$-\frac{1}{4}$,
∴当$-\sqrt{2}≤$t$≤-\frac{1}{4}$上时,函数g(t)是单调递减.
∴当$-\frac{1}{4}≤t≤\sqrt{2}$上时,函数g(t)是单调递增.
∴g($\sqrt{2}$)max=$\frac{1}{2}+\sqrt{2}$
故答案为:$\frac{1}{2}+\sqrt{2}$.
点评 本题考查了三角函数性质及化解能力,转化思想和换元法.利用了二次函数的性质.属于基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
10.直线y=$\frac{1}{2}$x+b是曲线y=ln x(x>0)的一条切线,则 实数b的值为( )
| A. | 2 | B. | ln 2+1 | C. | ln 2-1 | D. | ln 2 |
7.若$tan(θ+\frac{π}{4})=3$,则cos2θ+sin2θ=( )
| A. | $\frac{4}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{8}{5}$ | D. | 2 |
11.已知数列{an}中,a1=1,an+1=2an+1(n∈N*),则a4的值为( )
| A. | 31 | B. | 30 | C. | 15 | D. | 63 |
9.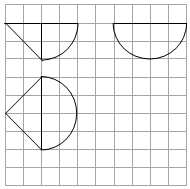 某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )
某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )
 某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )
某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )| A. | $\frac{28}{3}π$ | B. | 4π | C. | $\frac{10}{3}π$ | D. | $\frac{2}{3}+\frac{8}{3}π$ |
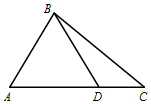 在△ABC中(图),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7},\overrightarrow{AD}=2\overrightarrow{DC}$.
在△ABC中(图),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7},\overrightarrow{AD}=2\overrightarrow{DC}$. 如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.
如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.