题目内容
(本小题满分12分)已知离心率为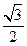 的椭圆
的椭圆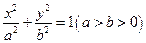 上的点到
上的点到
左焦点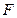 的最长距离为
的最长距离为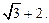
(1)求椭圆的方程;
(2)如图,过椭圆的左焦点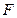 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦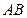 ,若点
,若点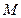 在
在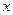 轴上,且使得
轴上,且使得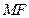 为
为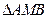 的一条内角平分线,则称点
的一条内角平分线,则称点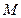 为该椭圆的“左特征点”,求椭圆的“左特征点”
为该椭圆的“左特征点”,求椭圆的“左特征点”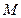 的坐标.
的坐标.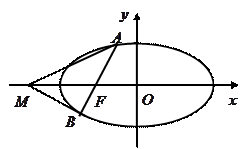
解:(1)由题意知: ,解得
,解得 ,
, ,
,
故椭圆的方程为 ,
,
其准线方程为 ………………………. ……………. ……………...4分
………………………. ……………. ……………...4分
(2)设 为椭圆
为椭圆 的左特征点,椭圆的左焦点为
的左特征点,椭圆的左焦点为 ,
,
可设直线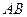 的方程为:
的方程为: ,
,
联立方程组 ,消去
,消去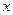 得
得 ,即
,即 ,
,
设 ,则
,则
∵ 被
被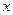 轴平分,∴
轴平分,∴ ,即
,即 ,
, ,
,
即 ,
,
∴ 于是,
于是,
∵ ,∴
,∴ ,即
,即 ,∴
,∴ .
.
解析

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
极坐标方程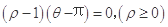 表示的图形是( )
表示的图形是( )
| A.两个圆 | B.一个圆和一条直线 |
| C.一个圆和一条射线 | D.一条直线和一条射线 |
在极坐标系中,圆 的圆心的极坐标是( )
的圆心的极坐标是( )
A. | B. | C.(1,0) | D.(1,π) |
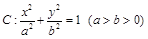 的左、右焦点分别为
的左、右焦点分别为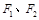 ,上顶点为
,上顶点为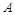 ,离心率为
,离心率为 ,在
,在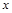 轴负半轴上有一点
轴负半轴上有一点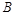 ,且
,且
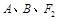 三点的圆恰好与直线
三点的圆恰好与直线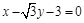 相切,求椭圆C的方程;
相切,求椭圆C的方程;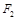 作斜率为
作斜率为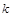 的直线
的直线 与椭圆C交于
与椭圆C交于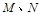 两点,在
两点,在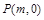 ,使得以
,使得以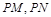 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出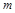 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.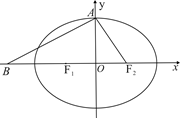
 的焦点分别为
的焦点分别为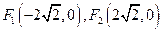 ,且过点
,且过点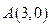 .
.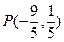 为椭圆
为椭圆 交椭圆
交椭圆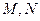 两点,且
两点,且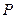 为线段
为线段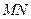 的中点,求直线
的中点,求直线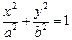 (
(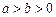 )上一点,F1,F2
)上一点,F1,F2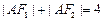 .
.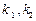 ,若存在常数
,若存在常数 使
使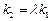 /,求直线CD的斜率.
/,求直线CD的斜率.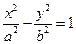 (a>1,b>0)的焦距为2c,直线
(a>1,b>0)的焦距为2c,直线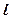 过点(a,0)和(0,b),且点(1,0)到直线
过点(a,0)和(0,b),且点(1,0)到直线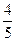 c.求双曲线的离心率e的取值范围.
c.求双曲线的离心率e的取值范围.
 在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
 ,
, ,
, ,
, ,点
,点 分别在线段
分别在线段
 上运动,且
上运动,且 ,设
,设 与
与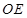 交于点
交于点 ,则点
,则点


