题目内容
【题目】若函数![]() 对任意的
对任意的![]() ,均有
,均有![]() ,则称函数
,则称函数![]() 具有性质
具有性质![]() .
.
(1)判断下面两个函数是否具有性质![]() ,并说明理由.①
,并说明理由.①![]() ;②
;②![]() .
.
(2)若函数![]() 具有性质
具有性质![]() ,且
,且![]() ,求证:对任意
,求证:对任意![]() 有
有![]() ;
;
(3)在(2)的条件下,是否对任意![]() 均有
均有![]() .若成立给出证明,若不成立给出反例.
.若成立给出证明,若不成立给出反例.
【答案】(1)①![]() 具有性质
具有性质![]() ;②
;②![]() 不具有性质
不具有性质![]() ,见解析;(2)见解析(3)不成立,见解析
,见解析;(2)见解析(3)不成立,见解析
【解析】
(1)①根据已知中函数的解析式,结合指数的运算性质,计算出![]() 的表达式,进而根据基本不等式,判断其符号即可得到结论;②由
的表达式,进而根据基本不等式,判断其符号即可得到结论;②由![]() ,举出当
,举出当![]() 时,不满足
时,不满足![]() ,即可得到结论;
,即可得到结论;
(2)由于本题是任意性的证明,从下面证明比较困难,故可以采用反证法进行证明,即假设![]() 为
为![]() 中第一个大于0的值,由此推理得到矛盾,进而假设不成立,原命题为真;
中第一个大于0的值,由此推理得到矛盾,进而假设不成立,原命题为真;
(3)由(2)中的结论,我们可以举出反例,如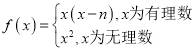 ,证明对任意
,证明对任意![]() 均有
均有![]() 不成立.
不成立.
证明:(1)①函数![]() 具有性质
具有性质![]() ,
,
![]() ,
,
因为![]() ,
,![]() ,
,
即![]() ,
,
此函数为具有性质![]() ;
;
②函数![]() 不具有性质
不具有性质![]() ,
,
例如,当![]() 时,
时,
![]() ,
,![]() ,
,
所以,![]() ,
,
此函数不具有性质![]() .
.
(2)假设![]() 为
为![]() 中第一个大于0的值,
中第一个大于0的值,
则![]() ,
,
因为函数![]() 具有性质
具有性质![]() ,
,
所以,对于任意![]() ,
,
均有![]() ,
,
所以![]() ,
,
所以![]() ,
,
与![]() 矛盾,
矛盾,
所以,对任意的![]() 有
有![]() .
.
(3)不成立.
例如,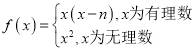
证明:当x为有理数时,![]() ,
,![]() 均为有理数,
均为有理数,
![]()
![]() ,
,
当x为无理数时,![]() ,
,![]() 均为无理数,
均为无理数,
![]()
所以,函数![]() 对任意的
对任意的![]() ,
,
均有![]() ,
,
即函数![]() 具有性质
具有性质![]() .
.
而当![]() 且当x为无理数时,
且当x为无理数时,![]() .
.
所以,在(2)的条件下,
“对任意![]() 均有
均有![]() ”不成立.
”不成立.
如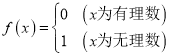 ,
,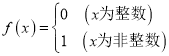 ,
,
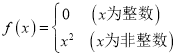 等.
等.

练习册系列答案
相关题目