题目内容
 如图,在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°且
如图,在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°且| AB |
| AC |
(I)求sin∠BAD的值;
(II)设△ABD的面积为S△ABD,△BCD的面积为S△BCD,求
| S△ABD |
| S△BCD |
分析:(I)首先在Rt△ABC中利用勾股定理求出AC=10,并且得出∠CAD的正弦、余弦,再结合AB=13且
•
=50,计算出∠BAC的正弦、余弦,最后利用两角和的正弦公式,可以求出sin∠BAD的值;
(II)根据正弦定理的面积公式,结合(I)中的数据分别求出三角形BAD、三角形BAC、三角形ACD的面积,最后求出三角形BCD,最后可以得到所要的两个三角形的面积的比值.
| AB |
| AC |
(II)根据正弦定理的面积公式,结合(I)中的数据分别求出三角形BAD、三角形BAC、三角形ACD的面积,最后求出三角形BCD,最后可以得到所要的两个三角形的面积的比值.
解答: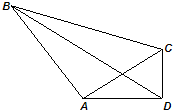 解:(I)在Rt△ADC中,AD=8,CD=6,
解:(I)在Rt△ADC中,AD=8,CD=6,
则AC=10,cos∠CAD=
,sin∠CAD=
…(1分)
又∵
•
=50,AB=13
∴cos∠BAC=
=
…(2分)
∵0<∠BAC<180°,
∴sin∠BAC=
…(4分)
∴sin∠BAD=sin(∠BAC+∠CAD)
=sin∠BACcos∠CAD+cos∠BACsin∠CAD=
…(6分)
(II)根据正弦定理的面积公式,可得
三角形BAD的面积为S△BAD=
AB•ADsin∠BAD=
…(8分)
同理,三角形ABC与三角形ACD的面积分别为:
S△BAC=
AB•ACsin∠BAC=60,S△ACD=24…(10分)
则S△BCD=S△ABC+S△ACD-S△BAD=
∴
=
…(12分)
 解:(I)在Rt△ADC中,AD=8,CD=6,
解:(I)在Rt△ADC中,AD=8,CD=6,则AC=10,cos∠CAD=
| 4 |
| 5 |
| 3 |
| 5 |
又∵
| AB |
| AC |
∴cos∠BAC=
| ||||
|
|
| 5 |
| 13 |
∵0<∠BAC<180°,
∴sin∠BAC=
| 12 |
| 13 |
∴sin∠BAD=sin(∠BAC+∠CAD)
=sin∠BACcos∠CAD+cos∠BACsin∠CAD=
| 63 |
| 65 |
(II)根据正弦定理的面积公式,可得
三角形BAD的面积为S△BAD=
| 1 |
| 2 |
| 252 |
| 5 |
同理,三角形ABC与三角形ACD的面积分别为:
S△BAC=
| 1 |
| 2 |
则S△BCD=S△ABC+S△ACD-S△BAD=
| 168 |
| 5 |
∴
| S△ABD |
| S△BCD |
| 3 |
| 2 |
点评:本题着重考查了向量在几何中的应用,属于中档题.解题过程中同时运用了正弦定理的面积公式和向量数量积的公式,是高考中的常考知识点.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 如图,在四边形ABCD中,△ABC为边长等于
如图,在四边形ABCD中,△ABC为边长等于 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC= 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=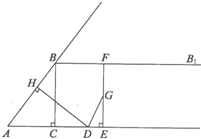 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒. (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,