题目内容

已知点A（2，8）、B（x1,y1）、C（x2,y2）在抛物线y2=2px上，△ABC的重心与此抛物线的焦点F重合（如图）.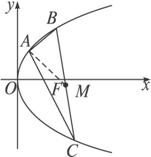

（1）写出该抛物线的方程和焦点F的坐标；

（2）求线段BC的中点M的坐标.

解：(1)由点A（2，8）在抛物线y2=2px上，有82=2p·2，解得p=16.

所以抛物线方程为y2=32x,焦点F的坐标为（8，0）.

（2）如题图，由于F（8，0）是△ABC的重心，M是BC的中点，所以F是线段AM的定比分点，且=2.

设点M的坐标为（x0,y0),则

=8,=0,

解得x0=11,y0=-4,

所以点M的坐标为（11，-4）.

练习册系列答案
相关题目
精英家教网已知点A（2，8），B（x1，y1），C（x2，y2）在抛物线y2=2px上，△ABC的重心与此抛物线的焦点F重合（如图）
（Ⅰ）写出该抛物线的方程和焦点F的坐标；
（Ⅱ）求线段BC中点M的坐标
（Ⅲ）求BC所在直线的方程．
已知点A（2，8），B（x1，y1），C（x2，y2）在抛物线y2=2px上，△ABC的重心与此抛物线的焦点F重合（如图）
（I）写出该抛物线的方程和焦点F的坐标；
（II）求线段BC中点M的坐标
（III）求BC所在直线的方程．
已知点A（2，8），B（x1，y1），C（x2，y2）在抛物线y2=2px上，△ABC的重心与此抛物线的焦点F重合（如图）
（I）写出该抛物线的方程和焦点F的坐标；
（II）求线段BC中点M的坐标
（III）求BC所在直线的方程．
已知点A（2，8），B（x1，y1），C（x2，y2）在抛物线y2=2px上，△ABC的重心与此抛物线的焦点F重合（如图）
（I）写出该抛物线的方程和焦点F的坐标；
（II）求线段BC中点M的坐标
（III）求BC所在直线的方程．

已知点A（2，8），B（x1，y1），C（x2，y2）在抛物线上，△ABC的重心与此抛物线的焦点F重合（如图）

（1）写出该抛物线的方程和焦点F的坐标；

（2）求线段BC中点M的坐标；

（3）求BC所在直线的方程.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网